『高性能计算』通用矩阵乘法GEMM及其优化概述

每日心情是汇编和组成原理知识都还给老师了 🤡

由于矩阵乘的具体实现基本上是大量的乘加运算，在没有高性能的矩阵乘计算库之前，落到高级语言上还得用嵌套循环来实现，因此矩阵乘对计算资源的消耗是很大的。除了计算机体系结构的不断更新外，软件优化方面对此也有大量的研究工作。一般来说的工作是：

• 结合实际场景，计算出性能最高的指令排布方式，然后手写这部分乘加计算的汇编
• 编译优化，在编译器层级完成自动并行化、循环优化等工作，加速计算
• 开发相关的高性能计算库（如 OpenBLAS 等），让用户直接调用一些常见规模的矩阵乘法，落到具体实现的话本质上也是手写汇编

讨论通用矩阵乘（General Matrix Multiplication，GEMM）的优化，实际上就是讨论如何设计一组针对给定规模和场景（稀疏 or 稠密，是否三角等）矩阵乘的高性能计算指令。

基于算法分析的优化

根据矩阵乘法的计算特性，可以从数学的角度做优化。

矩阵乘法的计算复杂性

在理论计算机科学中，矩阵乘法的计算复杂性决定了矩阵乘法的运算速度。最朴素的办法当然是使用三层循环，复杂度为  .一些数学方法的使用让它的计算复杂度得以下降，目前最好的方法可以达到  。最经典的优化算法是 Strassen 矩阵分块算法，其基于分治的优化思想非常具有启发性。

Strassen 算法

关键是引入中间矩阵，用 11 次额外的加减运算代替了一次乘法运算。

对于朴素的分块，我们知道矩阵运算可以简化成以下形式：

然而这种计算并没有在本质上减少乘法运算的规模。因此，Strassen 算法引入了以下的中间矩阵，使得计算最终简化为 7 次乘法：

此处还可以进行一些优化，减少矩阵加法的次数。可以使用 Winograd 发现的如下形式优化算法：

其中，

基于体系结构的通用优化

也叫软件优化方法，是结合具体计算的特性（例如矩阵的规模）和计算机体系结构的特征，设计出的针对性优化方法，基本思路是数据分块和在多级存储上进行高效的数据搬运 —— 这其实是 HPC 优化的重要思想，也就是：

1. 如何改善访存局部性，让数据放在 更近 的存储上掩盖计算的延时，从而减少内存墙的影响
2. 如何利用硬件的并行特性，高效执行计算

how-to-optimize-gemm 介绍了如何采用各种优化方法，将最基础的计算改进了约七倍。其基本方法是将输出划分为若干个子块，以提高对输入数据的重用。总计而言，采用的是以下几种通用的优化思路：

• 大量使用寄存器，减少访存
• 向量化访存和计算
• 重新组织内存以使得地址连续

更细节的调优方法就与具体的硬件架构相关了。

分块原理：使用寄存器减少访存

分块的基本动机是，既然每次迭代都需要重复存取数据，那么在 一次迭代 中计算目标矩阵的一个 Block 而不是某个元素就明显可以 复用 一部分数据（对于这些可复用的数据，处理策略是存储在寄存器中，减少访存次数），进而避免一些冗余的存取操作。这种策略也被称为 寄存器分块 （与之对应的一个概念是 cache 分块 ，比较复杂，后面再说）。

例如，对以下这种情况，假如一次迭代可以计算一个 1 x 4 的 Block 而不是一个元素，那么在那一次迭代内，读取到的矩阵 A 的第二行元素就可以复用。

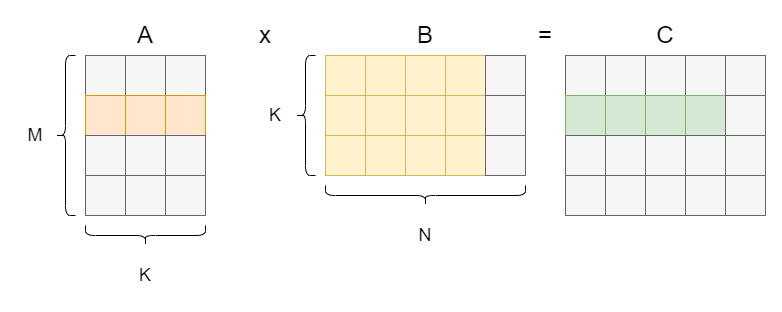
这段计算表示成伪代码可以写成（感觉伪代码形式更好理解）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

for (int m = 0; m < M; m++) {
	for (int n = 0; n < N; n += 4) {
		C[m][n + 0] = 0;
		C[m][n + 1] = 0;
		C[m][n + 2] = 0;
		C[m][n + 3] = 0;
		for (int k = 0; k < K; k++) {
			int curA = A[m][k];
			// 读取到寄存器中，实现 A 的访存的数据复用 (4 -> 1)
			C[m][n + 0] += curA * B[k][n + 0];
			C[m][n + 1] += curA * B[k][n + 1];
			C[m][n + 2] += curA * B[k][n + 2];
			C[m][n + 3] += curA * B[k][n + 3];
		}
	}
}

一般我们把最内层的循环称为 计算核 （micro kernel）。

显然，对 B 也可以实现访存的复用：

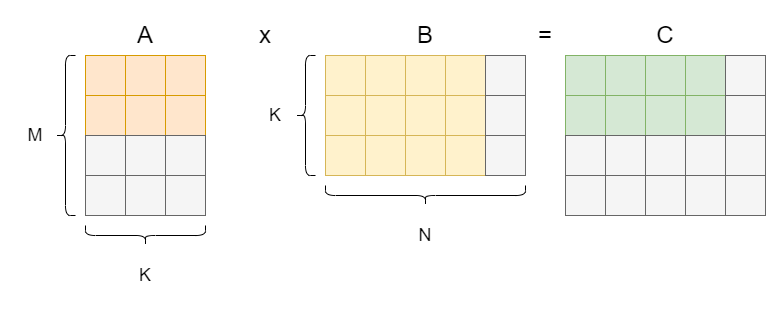
此时的情形表述为伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

for (int m = 0; m < M; m += 2) {
	for (int n = 0; n < N; n += 4) {
		C[m + 0][n + 0] = 0;
		C[m + 0][n + 1] = 0;
		C[m + 0][n + 2] = 0;
		C[m + 0][n + 3] = 0;
		C[m + 1][n + 0] = 0;
		C[m + 1][n + 1] = 0;
		C[m + 1][n + 2] = 0;
		C[m + 1][n + 3] = 0;
		for (int k = 0; k < K; k++) {
			int curA0 = A[m + 0][k];
			int curA1 = A[m + 1][k];
			// 读取到寄存器中，实现 A 的访存的数据复用 (8 -> 2)
			int curB0 = B[k][n + 0];
			int curB1 = B[k][n + 1];
			int curB2 = B[k][n + 2];
			int curB3 = B[k][n + 3];
			// 读取到寄存器中，实现 B 的访存的数据复用 (8 -> 4)
			C[m + 0][n + 0] += curA0 * curB0;
			C[m + 0][n + 1] += curA0 * curB1;
			C[m + 0][n + 2] += curA0 * curB2;
			C[m + 0][n + 3] += curA0 * curB3;
			
			C[m + 1][n + 0] += curA1 * curB0;
			C[m + 1][n + 1] += curA1 * curB1;
			C[m + 1][n + 2] += curA1 * curB2;
			C[m + 1][n + 3] += curA1 * curB3;
		}
	}
}

具体到 GPU 的执行中，在分块后是先将 A 和 B 中参与当前迭代运算的小矩阵（图中橘色和黄色的部分）取到 shared memory 中，之后各个线程再将 shared memory 中的数据存入寄存器中进行计算。设 A 中小矩阵的规模为  ，B 中小矩阵的规模为  ，且此时一个 block（图中绿色部分）中每一个线程负责一个元素的计算，这就说明一个 block 需要对 shared memory 进行  次读操作，从 shared memory 中取数的时延还是不可忽视的。此时，我们进一步考虑对 shared memory 进行分块。

通过上面两个样例，我们可以看到对 M 层循环和  N 层循环，通过修改迭代的步进长度来展开循环后，都可以得到一定程度的数据复用改进（具体而言，步长变为  时可以减小访存次数到原来的  倍）。目前为止，这个改进都是针对输出的两个维度做的，对于最后一层，也就是中间那个维度 K （被称为削减维度，Reduction），实际上也可以尝试做展开，实现更激进的访存复用：

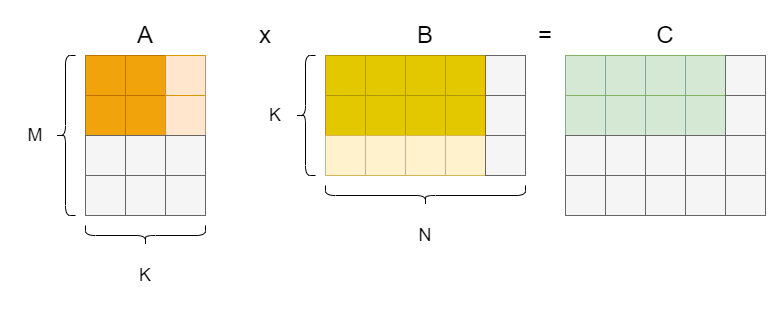
表述成伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

for (int m = 0; m < M; m += 2) {
	for (int n = 0; n < N; n += 4) {
		C[m + 0][n + 0] = 0;
		C[m + 0][n + 1] = 0;
		C[m + 0][n + 2] = 0;
		C[m + 0][n + 3] = 0;
		C[m + 1][n + 0] = 0;
		C[m + 1][n + 1] = 0;
		C[m + 1][n + 2] = 0;
		C[m + 1][n + 3] = 0;
		for (int k = 0; k < K; k += 2) {
			int curA00 = A[m + 0][k];
			int curA10 = A[m + 1][k];
			int curA01 = A[m + 0][k + 1];
			int curA11 = A[m + 1][k + 1];
			
			int curB00 = B[k][n + 0];
			int curB01 = B[k][n + 1];
			int curB02 = B[k][n + 2];
			int curB03 = B[k][n + 3];
			int curB10 = B[k + 1][n + 0];
			int curB11 = B[k + 1][n + 1];
			int curB12 = B[k + 1][n + 2];
			int curB13 = B[k + 1][n + 3];
			
			int c00 = c01 = c02 = c03 = 0;
			int c10 = c11 = c12 = c13 = 0;
			
			c00 = curA00 * curB00 + curA01 * curB10;
			c01 = curA00 * curB01 + curA01 * curB11;
			......
			c13 = curA10 * curB03 + curA11 * curB13;
			
			
			C[m + 0][n + 0] += c00;
			C[m + 0][n + 1] += c01;
			C[m + 0][n + 2] += c02;
			C[m + 0][n + 3] += c03;
			
			C[m + 1][n + 0] += c10;
			C[m + 1][n + 1] += c11;
			C[m + 1][n + 2] += c12;
			C[m + 1][n + 3] += c13;
			// 将部分和累加在寄存器中
			// 导致原本完成这些操作需要对 C 进行的 16 次访存变成 8 次
		}
	}
}

鉴于现代处理器出色的 SIMD 能力，实际上可以采用的分块策略可以比示例更加激进。此处还可以做一个 避免乘法 的优化，也即保存指针，使用指针偏移完成形如 …[n + 0], …[n + 1] 的工作。

而显然，我们可以看到图中举的例子是 不对齐 的，这样的 Block 策略显然不是最优的数据复用策略。实际应用中应当考虑矩阵乘的规模和具体的体系结构，采取合适的 Block 规模设计（最终目标是提升计算访存比）。不同的分块大小在不同 shape 的矩阵乘法应用上性能各有优劣。

此处可以参考 旷视 的博客。

寄存器重映射

考虑上一节中最后一个优化，由于每一个线程（一个线程处理一轮迭代）都使用了相当规模的寄存器，此时我们不得不考虑寄存器之间的 bank conflict 问题。或者说，所有计算密集型的算子都需要考虑这个问题。

寄存器的 bank conflict 是指在并行计算中，多个线程同时访问同一个寄存器 bank 时发生的冲突。在现代处理器中，寄存器被组织成了多个 bank ，每个 bank 可以同时访问不同的寄存器。然而，如果多个线程同时访问同一个 bank 中的不同寄存器，就会发生 bank conflict 。如果一条指令的的源寄存器有 2 个以上都来自同一个 bank ，产生了 bank conflict，指令就会重发射，浪费掉一个时钟周期。

为了避免寄存器的 bank conflict ，可以通过重新安排寄存器的分配方式来减少冲突，这个策略称为寄存器重映射。

数据预取 prefetch：掩盖访存延迟

其实很好理解，就是排指令计算的软流水的时候，可以 “重叠” 一部分操作，让一部分取数据操作放在上一部分的计算操作中同时进行，避免在单次迭代中出现计算单元因取数而停下来等待的延迟行为。

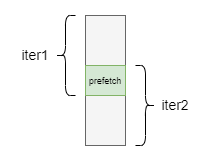
具体而言，当 Block 进行第 k 轮迭代时，需要对小矩阵  和  进行计算，此时我们提前将  和  取到 shared memory 中，这样进行第 k + 1 轮迭代的时候，计算单元就无需等待将该轮次迭代需要的小矩阵从 global memory 搬运过来的时间了。对于寄存器，也可以采取 prefetch 策略进行优化。

向量化与内存组织重排

对于带有 SIMD 支持的处理器，访存和计算都可以向量化（提供了向量寄存器），此时可以利用向量特性提高计算性能。具体而言，需要对之前朴素分块计算中的指令进行 重排 ，使得对 A、B 和 C 矩阵的 访存连续 ，然后将对应的访存和计算向量化，如下图所示（图例是行优先存储的）。

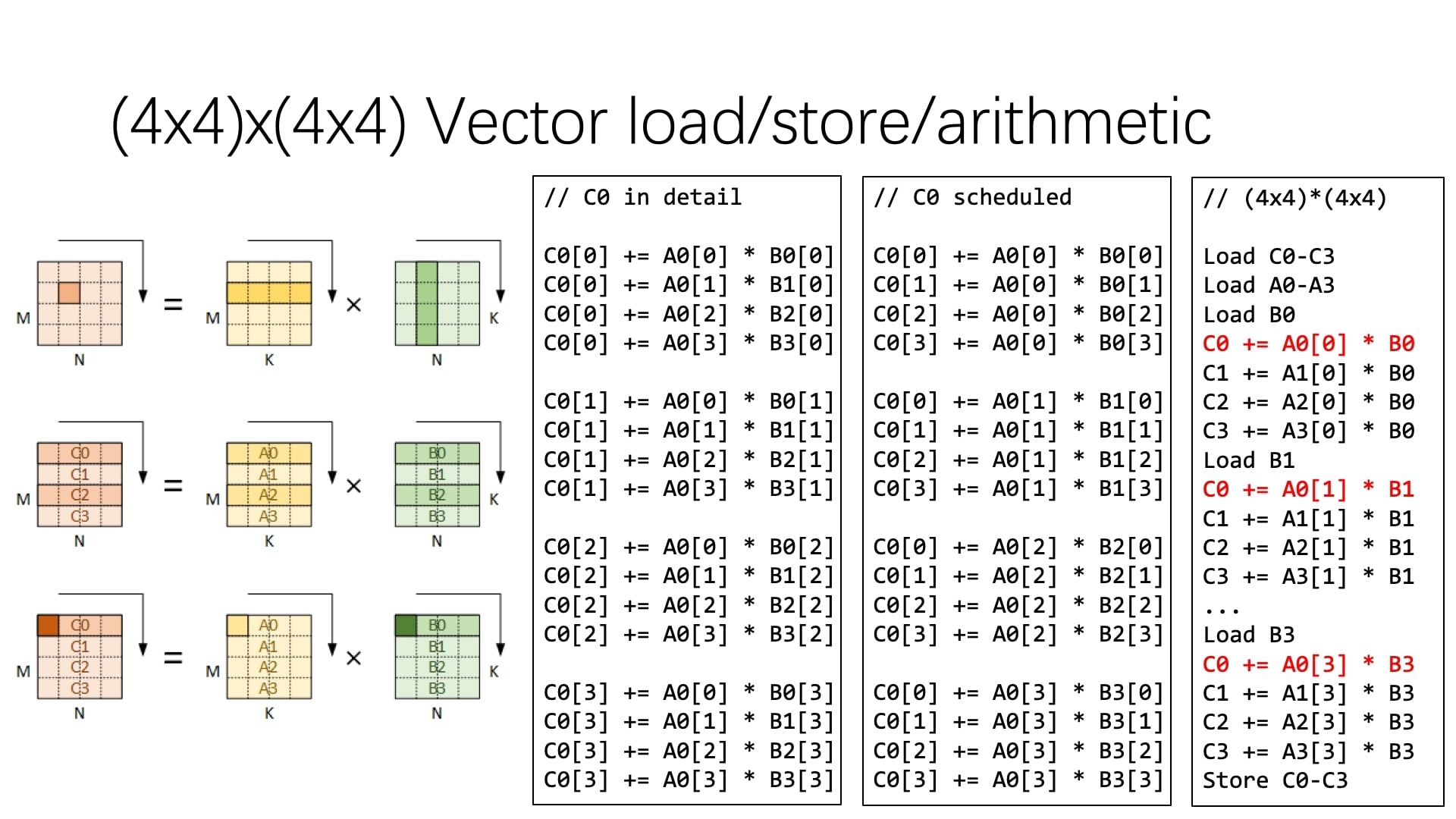
只不过要注意的是，向量化内存加载必须讨论的问题是访存连续性 —— 如果不进行重排，向量化内存加载时会频繁发生高速缓存缺失（cache miss）现象，浪费很多时钟周期。

TODO：

• GotoGEMM 论文：Anatomy of High-Performance Matrix
  Multiplication
• OpenBLAS GEMM 优化