『编译优化』Automatic Parallelization: 自动并行化

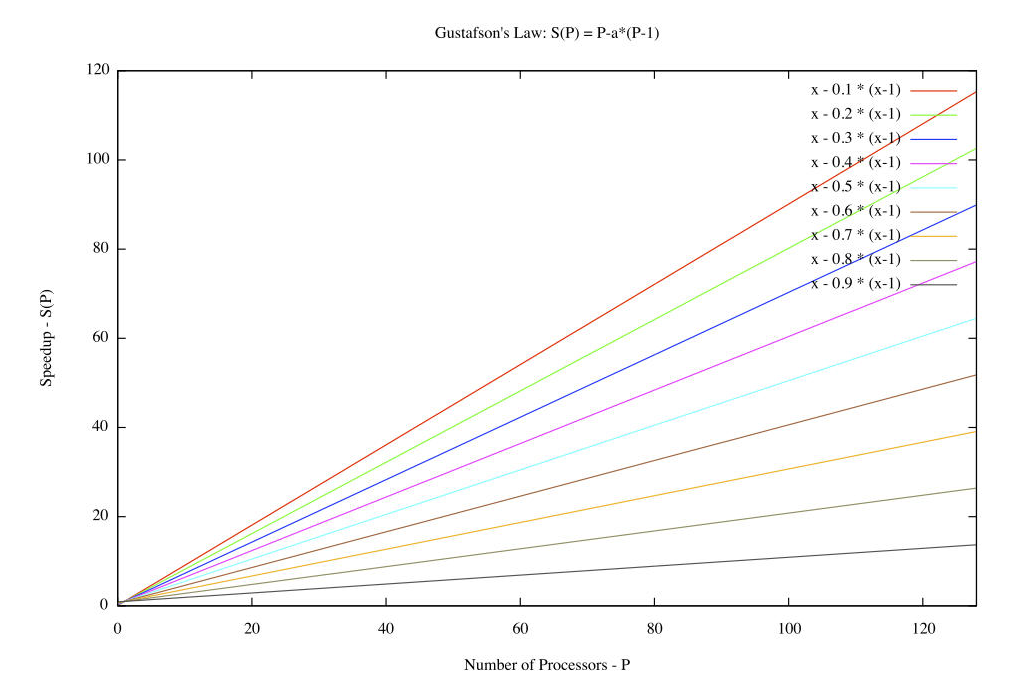
我们知道如果程序可以利用额外的处理器来解决更大规模的问题，那么它就可以表现出可扩展的并行性（Scalable Parallelism）—— 这个术语指代它符合古斯塔夫森定律。

在计算机体系结构中，以假想任务在单核计算机上运行为基准，古斯塔夫森定律给出了理论上可以从并行计算中获得的任务执行时间的加速比，如下图所示。换句话说，如果一个任务运行在串行机器上，它是一个已经并行化的任务理论上的“减速”。

并行化编译面临的任务是：给定一个在单处理机上运行较长的串行程序和一台具有多个处理器可同时工作的并行计算机，目的是将串行程序分解成若干个能并行执行或至少能重叠执行的代码段，使其在并行机上能较快地运行。所以并行编译器主要工作就是寻找代码的并行性，然后将其调度在并行机上高速正确地执行。

手工并行化代码非常耗时。幸运的是，有并行编译器可用 —— 这些编译器可以将串行源代码转换为并行代码，提高其运行效率。并行编译器首先会像传统编译器那样将源代码转换成一种中间表示形式，比如抽象语法树（AST）或分层任务图（HTG）。然后，它将以一种将程序的串行流尽可能转换为正确的并行流的方式，对 IR 执行指令重排等转换和优化，从而将工作分散到处理器的多个核上。然后，它会将 IR 转换为可并行执行的代码，以便将其编译为二进制代码。

这意味着，并行编译，也即并行代码生成的工作包括了两个部分：针对 IR 的并行转换和优化，针对并行代码生成的代码调度。前者被称为并行程序分析，包括向量化、并行化、指令重排等工作，之前介绍的树高平衡优化就属于这一部分；后者则属于后端，被称为并行代码生成，包括寄存器分配、负载平衡、现场切换等技术。

自动并行化 是并行编译的核心思维。R. Eigenmann 在他的课程 Parallelizing Compilers for Multicores 上发表了 “优化编译器是宇宙的中心” 的意见，实在是所见略同，在性能越重要的地方，优化编译器就越重要，因而关注高性能计算的并行编译（Parallelization）就是优化编译器中的重中之重（另一个重点是 Privatization，关注数据的局部化，因为使用全局变量的开销显然更大，而实际上，很多局部化方法也是为并行化服务的）。

程序分析：探索程序中的并行性

Data Dependence Test（DDT）：数据依赖分析

检测程序中的数据依赖（Data Dependence）是自动并行化的实现核心。在讨论树高平衡优化的时候我们已经强调过，只有 独立 的指令才满足可并行执行的条件，同时，不同的候选树之间也因为数据依赖存在着优先级排序关系，因此，分析程序中的数据依赖关系是为了保证自动生成的并行代码的正确性 —— 实际上，数据依赖昭示了几乎所有并行化 CodeGen 技术的 合法性 。

举例而言：如果一个循环在任意两个迭代之间没有数据依赖关系，那么不同迭代轮次显然可以安全地并行执行。此处讨论循环的可并行性是 make sense 的。根据有关调研，在学术 / 工程应用中，循环 结构的并行执行始终是最重要、收益最大的。

首先给出数据依赖的定义。两个数据引用之间存在数据依赖关系，当且仅当：

• 两个引用访问了相同的存储位置
• 其中至少有一个访问是写访问

在单次迭代内，数据依赖分析很简单，因此对于所有不涉及循环结构的基本块而言数据依赖分析也不是什么难题，只要按照上面两条规则分析就可以了，使用 SSA 更是提供了很大的方便。但涉及到循环所有迭代之间的依赖，问题就变得比较困难。以下面这段代码为例：

1
2
3
4

for (int i = 0; i < n; i++) {
	a[4 * i] = ...;
	... = a[2 * i + 1];
}

此时我们要解决的数据依赖关系就是：对于任意 ，是否存在 ？如果存在，显然那两个对应的迭代之间就存在数据依赖了，并行执行可能会有正确性问题。将其一般化，针对循环并行化问题，我们要解决的问题可以抽象成：

给定两个下标函数 和 ，并给出循环的上界和下界，是否存在 ？

为了解决这个问题，我们首先给出以下术语：

• 距离向量：表示数据依赖的 source 和 sink 之间相隔多少个迭代
• 方向向量：基本上是距离向量的符号，有 (<, =, >) 或者 (-1, 0, +1) 的表示方法，表示依赖关系的先后次序
  • 依次为从较早循环到较晚循环、在同一循环内、从较晚循环到较早循环
• 循环传递依赖（或称跨迭代依赖）和非循环传递依赖（或称循环独立依赖）：也就是循环关系是否在单次迭代内
  • 显然，对于我们需要检测的循环并行性，只有跨迭代的依赖关系才重要，而那些循环独立依赖，则对类似指令重排和循环分布这样的优化比较重要，之前分析的大部分也是这些优化

使用这些术语，可以先将上面的例程抽象成如下的向量表示形式：

1
2
3
4

for (int i = 0; i < n; i++) {
	X(4 * i + c1) = ...;
	... = X(2 * i + 1 + c2);
}

需要解决的依赖分析问题则被抽象为：

更复杂的情况：

这里注意：

• 几乎所有的 DDT 都期望 等系数是整数常数。这种下标表达式称为 仿射 表达式
• 迭代的轮次数 从整数讨论到了不定方程

一种判定跨迭代的算法叫做 GCD Test，其思路是：对于方程 ，当且仅当 可以整除 时，我们认为对应的指令存在跨迭代依赖。

这一算法简单但不准确，还有很多其他种类的算法和它们的变种，例如 Banerjee(-Wolfe) Test（讨论两个数据引用访问的下标范围，如果不重叠就认为不依赖）、Omega Test（最准确的）、Range Test（上面提到的算法基本上都是仿射的，即要求系数是整数常数，当然必须存在非线性和基于符号值的 DDT 方法，Range Test 是其中一个） 等。（尼玛怎么一堆待填的坑

这段话揭示了一个现实情况：如今 DDT 并不成熟，而且面临很多工程的或者学术的问题。具体而言，可能面临以下的问题：

• 更好地处理多维数组和循环嵌套
• 添加对非步长为 1 的循环和不同循环下界的处理能力
• 如何处理符号值系数和边界
  • 涉及符号分析
• 忽略局部变量和归约操作中的依赖关系
• 生成依赖关系向量（DD vectors）
• 标记可并行执行的循环

并行化分析方法

在 IR 阶段，大约有以下这些基本的并行化分析方法 —— 它们很难被称为并行化方法，基本思路本质上是对程序做可并行化的分析，为后面代码生成阶段生成真正可并行执行的代码做一些准备，但还是属于中端优化的范畴。我们可以在具体的算法中看到，基本上都是 程序分析 的内容。

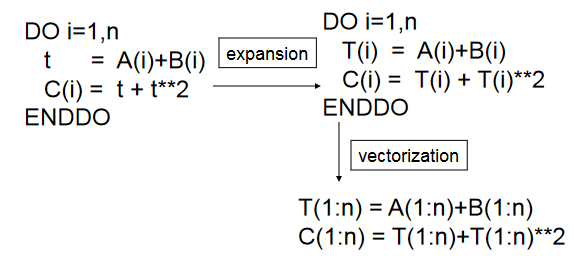
标量扩展（Scalar Expansion）

旨在减少循环中的内存访问开销，采用的一般技术是局部化（ Privatization ）。

具体而言，编译器会将标量变量的计算结果保存在一个临时变量中，并在每次迭代时更新该临时变量。这样一来，循环内部就不再需要每次迭代都进行内存读取和写入操作。

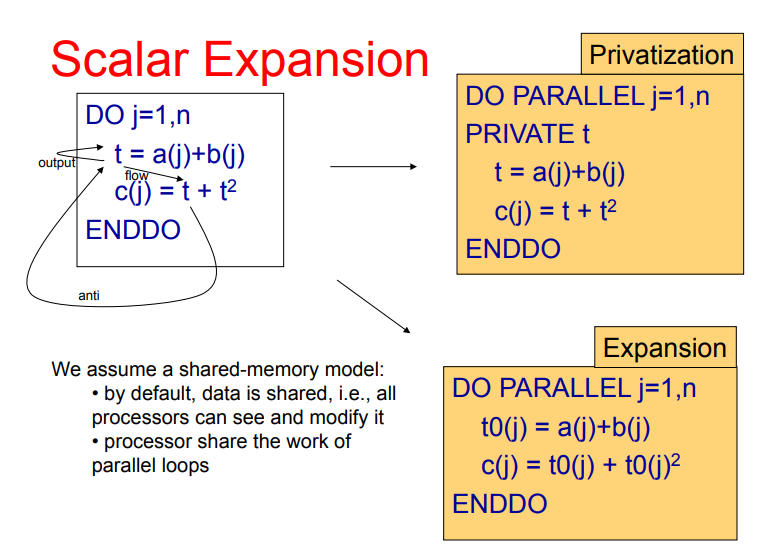
上图的例子给的是一个非常简单的变量局部化。当然，我们也可以讨论 数组局部化 ，在循环内部局部化一些循环外部数组的元素。此时，可能需要进行以下分析：

• 数组的 Def-Use 分析
• 下标范围的合并和相交分析

讨论多层嵌套循环内数组局部化的基本算法是：对于每个循环嵌套，从最内层开始分析循环的迭代。

• 对于循环中的每条语句，都找到其定义，将其添加到该循环现有的定义当中；
• 然后找到数组的使用，如果它们被一个定义覆盖了，就将此数组元素标记为对该次迭代可私有化，否则将其标记为在该次迭代中向上暴露；
• 最后，聚合所有的定义和向上暴露的使用范围，也就是从单次迭代的范围扩展到整个迭代空间，将他们标记为该循环的 Defs 和 Uses 。

归约并行化（Reduction Parallelization）

指在循环中对一系列值（根据定义可知，这些值都是归纳变量）进行聚合（如求和、求积等）。顾名思义，归约并行化的目标就是将归约操作转换为并行操作，以便在多个处理单元上同时执行计算操作。

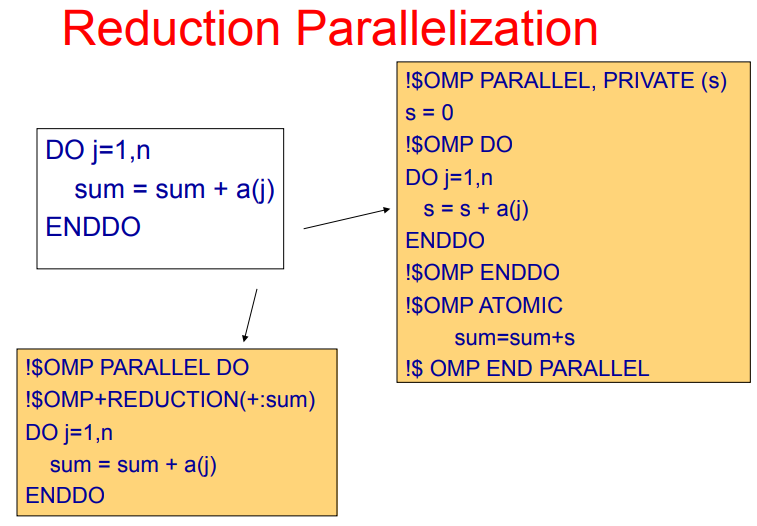
一个实现归约并行化的优化 Pass 的具体流程是：

• 识别归纳变量
• 识别可归约操作
  • 以上两步的具体实现在归纳变量削弱的笔记中都写过了
• 变量局部化
• DDT
• 对 DDT 分析中合法的操作做并行化

归纳变量替换（Induction Variable Substitution）

归纳变量是指在循环中使用的按照固定模式递增或递减的变量。通过归纳变量替换，可以将循环中的归纳变量替换为一个等价的表达式，以减少不必要的变量操作，从而提高性能。

详见归纳变量削弱优化：『中端优化』Strength Reduction: 运算符强度削减

循环交换（Loop Interchange）

指改变循环的嵌套顺序，以便更好地利用计算资源，例如经典的在 C 语言中交换循环嵌套顺序大大加速执行的那个例子。通过重新排列循环的顺序，可以改善数据局部性和内存访问模式，从而提高程序的性能。

前向替换（Forward Substitution）

指在循环中使用常量或已知值来替换变量的引用，减少运行时的计算开销。

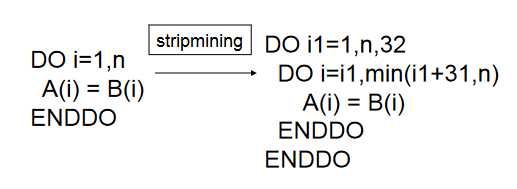
条带分割（Stripmining）

基础思路是将一个大循环拆分成多个较小的循环，以减少循环迭代次数，同时揭示更多可并行执行的循环的可能性。（跟代码生成阶段的循环分块技术很像，但有一定的区别）

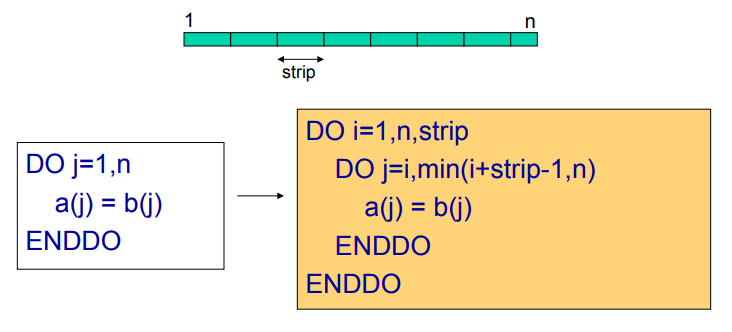
其实所谓 分割 的本质就是找到一个合适的条带长度 strip ，使得不同条带之间的循环过程在内存空间的角度上互不影响（直观理解：地址空间不重叠），从而达成并行执行的目的。在这里，我们可能可以通过类似过程间常量传播这样的过程间方法发掘出一些优化的时机，例如下图：

如果 m > 100 ，那么显然可以构造一个条带长度为 100 的分割，实现并行优化。

循环同步（Loop Synchronization）

是指在并行循环中进行数据同步的操作（比如 wait 一下保证数据在其他并行任务中被更新了），以确保正确的结果。

递归替换（Recurrence Substitution）

调用一个等价的递归函数，代替原本的循环。

可以看到，基本的优化思路都是：减少计算开销和内存访问开销，以及提高 并行性 和 局部性 。

代码生成：将并行性映射到不同机器

针对共享内存的机器（如绝大多数多核处理器）

均为并行化操作，讨论的多为 MIMD（多指令多数据）级别的优化。

循环融合（Loop Fusion）

旨在将多个 相邻 的循环合并为一个循环，是 循环展开 优化的逆过程。通过将循环融合在一起，可以减少循环迭代的开销，提高程序的性能和效率。

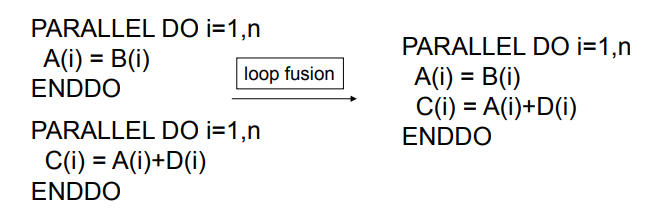
当多个循环之间存在依赖关系时，将它们合并为一个循环可以减少循环迭代的次数，从而减少循环控制指令的执行次数。这样一来，可以减少指令级并行的开销，提高处理器的流水线利用率，并减少 分支预测 错误的可能性。

循环融合还有助于提高数据局部性。当多个循环被合并为一个循环时，循环体内的数据访问模式可能会发生变化，从而改善数据的局部性。这可以减少对内存的访问延迟和带宽需求，提高缓存的命中率，从而提高程序的整体性能。

需要注意的是，循环融合并非在所有情况下都能带来性能提升。在某些情况下，循环融合可能会导致循环体内的计算和内存访问变得更加复杂，从而降低性能。此外，循环融合也可能增加代码的复杂性，降低代码的可读性和维护性。

因此，在进行循环融合优化时，编译器需要综合考虑循环之间的依赖关系、数据局部性以及代码的复杂性，以确保优化的效果超过潜在的开销增加。

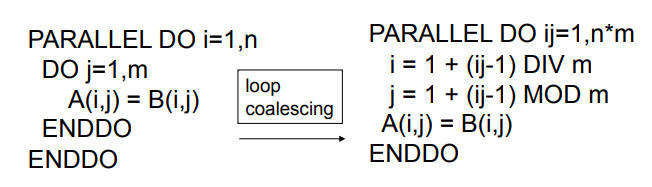
循环合并（Loop Coalescing）

与循环融合的概念不同，用于将嵌套的循环合并为一个深度更浅但更大的循环。显然，它增大了一个并行循环的迭代次数，这一特性可以被用来做 负载均衡 的工作。

循环分块（Loop Blocking）

又称 Loop Tiling ，一种用于改善数据局部性和缓存效率的循环优化技术。它通过将大型循环划分为更小的块或子循环来提高数据的局部性，减少对内存的访问延迟，并提高缓存的命中率。因为其实现基本上就是条带分割 + 循环交换的结合，因此有些地方也把它称为 strip mine and interchange 。由于它实际上已经是自动并行化的主流技术实现，很多时候我们提到的循环嵌套优化（Loop Nest Optimization），就专指循环分块。

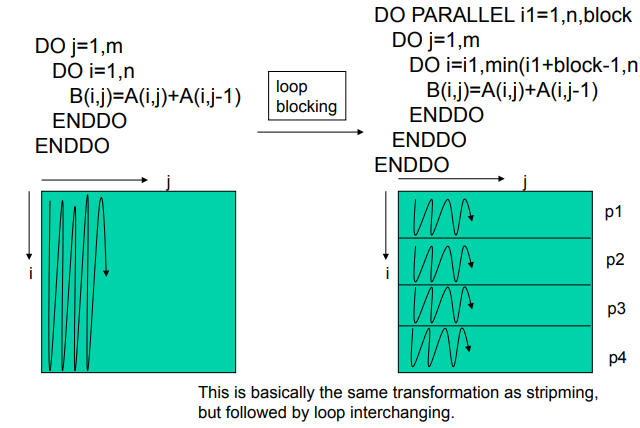
它的基本思想是将循环中的连续迭代分组为更小的块或子循环。每个块内的迭代在内部执行，这样可以增加数据的重用，并减少对内存的频繁访问。块长度必须足够小，使得使用和重用之间的所有数据引用都能被放入缓存。

此处需要注意，如果缓存是共享的，那么所有处理器都会同时使用它。因此，有效的缓存大小看起来更小，上述的块大小公式将改写为：

循环分块对于 多级缓存 的效果尤为明显。由于块的尺寸更小，它们更容易适应缓存的大小，从而提高缓存的命中率。这对于具有多级缓存结构的现代处理器来说尤其重要，因为它们的缓存层次结构通常具有不同的大小和访问延迟。

这一优化可能会增加代码的复杂性，因为需要引入额外的循环和索引计算。此外，其优化效果取决于硬件的数据访问模式和循环的性质。

是编译优化论文中经常看到的优化技术，感觉是待填的大坑 ……

循环交换（Loop Interchange）

改变循环嵌套的执行顺序，以改善数据的局部性、提高缓存的命中率，应该是大众所熟知的一项优化。当具有多个循环嵌套时，循环交换可以改变数据访问的顺序，从而使访问内存的模式更加连续，减少对内存的访问延迟和带宽需求。

循环交换还可以影响循环并行化的粒度和效果。在某些情况下，循环交换可以改变循环之间的依赖关系，从而使得并行化更容易实现。通过交换循环的执行顺序，可以改变数据的依赖关系，提供更多的并行化机会。

同样的，它必须受制于依赖关系合法性的约束。

循环拆分（Loop Distribution）

有时候我们需要通过拆分循环发掘可能的循环交换机会，如：

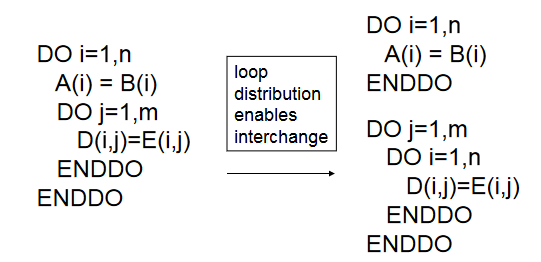
这同时也启示我们，在一个具有许多多层嵌套循环的程序中，可以通过拆分和交换发掘出大量的优化时机 —— 这是一个循环优化的重要议题。

单循环多级并行

本质上是上述的条带分割技术，只不过加入了处理器硬件本身的多级并行特性。

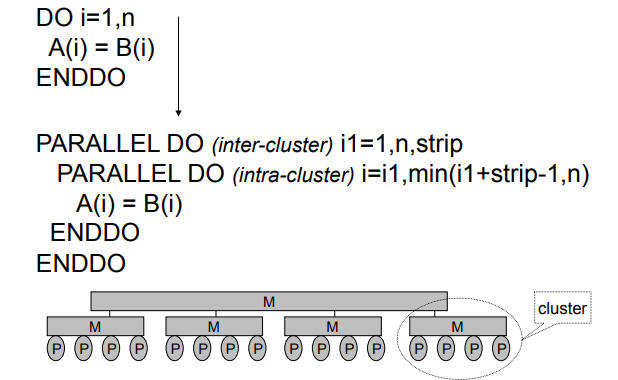
针对向量机

讨论基于 SIMD（单指令多数据）的优化，主要是利用向量指令实现一些并行化操作。向量化的基础是数据扩展（Expansion），这是一个与前面提到的标量扩展 —— 也就是变量私有化 —— 相反的概念，它往往需要将一个局部变量扩展成可用的向量，与简单的数据长度扩展有些区别。

SIMD 简介

SIMD（Single Instruction Multipile Data，单指令多数据）

传统的标量指令每次处理一个数据（SISD，单指令单数据），而向量指令（也叫 SIMD 指令）则每次处理一批数据，实现了一种细粒度的并行性，例如图像处理或者一些多媒体的应用 —— 这类应用需要对庞大的像素数据做同样的操作，向量指令在这种情形下可以极大地提高计算速度。有时还可以用向量寄存器来实现一些特殊的 CPU 寄存器或者内存，例如经典的超级计算机。超级计算机场景中还经常存在大规模的循环迭代，这也对并行执行存在很高的要求。

向量指令是在硬件功耗限制、单核主频速度提高陷入瓶颈的这一背景下提出的一种性能提升方法，它以及类似的性能提升方法更多地依赖体系结构的改进而非硬件的摩尔定律，一般来说有以下几种思路：

• 提高流水线效率
• 提高 Cache 存取效率
• 采用向量指令，提高向量长度
• 引入多核

向量化编程关注的是如何在软件层面上实现向量化，进而利用硬件的向量指令特性。

可以举一个经典的归约例子（也就是数组求和），为了利用可能存在的 SIMD 汇编代码，一次累加四个数据而非一个一个累加：

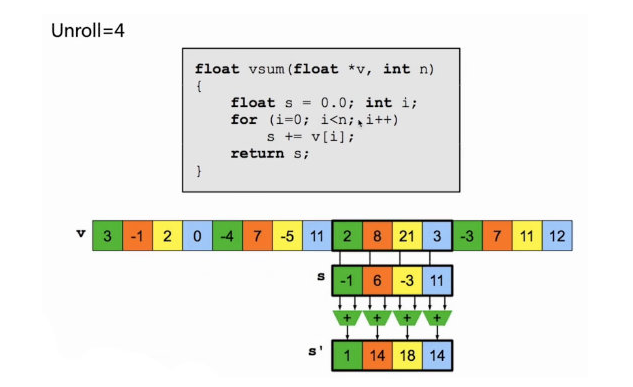
注意加到最后一步得到的实际上是一个向量化的中间结果，而非实际结果，还需要对它进行一次向量内部的累加。做了向量化处理后，源码可以写成这种形式：

1
2
3
4
5
6
7
8
9
10
11
12
13

float vsum(float *v, int n) {
	float vs[4] = {0.0, 0.0, 0.0, 0.0};
	float s = 0.0;
	int i;
	for (i = 0; i < n - 4; i += 4) {
		vs[0] += v[i];
		vs[1] += v[i + 1];
		vs[2] += v[i + 2];
		vs[3] += v[i + 3];
	}
	s = vs[0] + vs[1] + vs[2] + vs[3];
	return s;
}

所以基础的优化方法实际上就是寻找代码中的主循环，然后用向量化指令去处理主循环的步长，当然要记得做好边角处理。

一般似乎不怎么在高级语言层面上直接做向量化编程，而是写汇编。适于入门开发的是 ARMv8 Neon Intrinsic 编程。

向量化条带分割技术

也就是对经典的条带分割技术，将条带大小设置成可用的向量长度（可以是向量长度，或者能够并行执行的向量子块），进而实现多级并行。例如下面这个将单循环转换成双嵌套循环的例子可以实现两级并行，不同的长度为 32 的数据块之间可以实现并行的向量元素赋值操作。

向量流水线

关于向量指令，除了并行化执行，还有一个重要的点是：针对不同向量元素的操作可以 重叠 ，这就涉及到一个叫做 向量流水线 的技术。

向量流水线的工作原理是将一组连续的向量操作划分为多个子操作，并将这些子操作依次放入流水线的不同阶段，个人感觉思路跟 Stripmining 基本上是一样的。每个阶段都有自己的功能单元，并且可以同时处理多个数据元素。这样，当一个数据元素通过一个阶段时，下一个数据元素可以立即进入该阶段进行处理，从而实现并行执行。

然而，向量流水线也存在一些挑战和限制。首先，向量操作之间的依赖关系可能会导致数据冒险或控制冒险，需要使用相关技术来解决（或者通过计算方法避免依赖冲突）。此外，向量操作的长度和规模也会对流水线的性能产生影响，因为较长的向量操作可能需要更多的周期来完成。

程序分析进阶：过程间 DDT

实际上动机也很简单，就是利用过程间分析方法传播数据依赖信息，以发掘更多的向量化可能性。

例如，对于这类例子：

1
2
3
4
5
6
7

DO i=1, n
	call clear(a, i)
ENDDO

Subroutine clear(x, j)
	x(j) = 0
END

如果执行了过程间 DDT，就可以用向量化指令 x[1:n] = 0 来简化计算。

对于这类例子：

1
2
3
4
5
6
7
8

DO i=1, n
	a(i) = b(i)
	call dupl(a, i)
ENDDO

Subroutine dupl(x, j)
	x(j) = 2 * x(j)
END

可以简化成 a[1:n] = 2 * b[1:n] 这样的向量化指令。

过程间 DDT 包含以下基本策略（都是一些挺符合常理的一般化方法）：

• 子程序内联
• 将循环移入 callee 的程序中
  • 应该得经过一些分析，确保对应的 callee 只在循环中被调用，然后改造 callee 内部程序？
• 在 callee 中收集针对数组的访问信息，在针对 caller 的分析中使用这些信息
  • 可以看到，大部分存在并行优化时机的子程序都包含有数组特征，同时 call-site 存在于循环中，利于使用向量指令等做优化，因此探讨子程序的数组信息是有价值的
  • 涉及具体的符号分析算法，TODO

针对分布式内存的机器

分布式内存机器采用的是 SPMD（Single Program Multiple Data，单程序多数据）的执行模式，其实就是讨论 多处理器 机器。它天然采用并行计算的程序执行方案，将一个计算任务分成多个子任务，每个子任务在不同的计算节点上并行执行（本质上是同一个程序，不同的数据），最后将结果合并得到最终的计算结果。在分布式内存机器中，计算节点之间通过网络进行通信和数据交换，以实现任务的分配、数据的传输和结果的合并。这种程序执行方案可以充分利用分布式内存机器中的多个计算节点的计算能力，提高计算效率和吞吐量。在对应的软件程序中，程序使用 node _ id 选择要在每个参与的处理器上执行的子计算任务和需要访问的数据。

对于一个有 m 个计算节点的分布式内存机器，我们可以把 1 ~ n 循环问题简化成如下的形式：

1
2
3
4
5
6
7

// current processor: node_id
stripSize = round(n / m)
lowerBound = node_id * stripSize + 1
upperBound = min(lowerBound + stripSize - 1, n)
DO i=lowerBound, upperBound
	...
ENDDO

可以看到，针对分布式内存的机器，可能存在的优化问题是：

1. 如何排布数据的分布情况，可以使得计算更高效？
   1. 也就是选择 node_id 的问题
2. 不同计算节点之间存在通信和数据交换问题。如何安排它们的同步机制？
   1. 也就是不同 strip 之间同步的问题

数据分布问题

在分布式计算机上，数据的排布方式可以分为两种基础模式：

• 单一所有者模式（Single-Owner）：数据分布在参与计算的处理器的内存上
  • 给数据分配特定的计算节点，取数据的时候要找对应的计算节点
• 复制模式（Replication）：数据的多个版本被放置在某些或者全部计算节点上
  • 也就是说，取数据的时候是取版本，而不是取计算节点，这样一来，每个处理器本地的读写操作将是完全并行的

单一所有者模式的数据可能存在以下四种分布方式，其中，数字表示机器内处理器的序号：

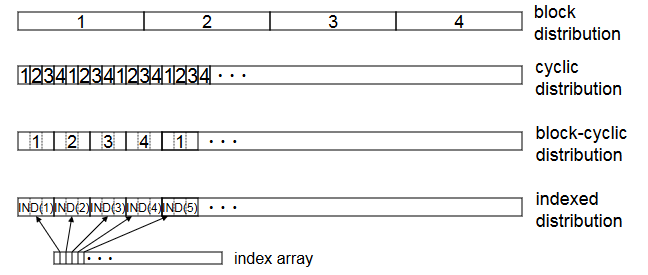
自动化数据排布是一个比较困难的全局优化问题，很多时候还是采用手工调优。

节点通信问题：消息生成（Message Generation）

不同于数据排布，节点通信问题上有表现比较好的自动生成方案。

首先讨论单一所有者模式下的消息生成。因为决定了数据分布方案后， lowerBound 和 upperBound 的大小就可以决定分配给每个计算节点的 strip ，而数组内部数据的分布又刚好跟循环迭代的分布情况相契合，这样为自动生成收发数据消息提供了一定的正确性保证。例如：

1
2
3
4
5

send(A(upperBound), cur_proc + 1)
receive(A(lowerBound - 1), cur_proc + 1)
DO i=lowerBound, upperBound
	B(i) = A(i) + A(i - 1)	// need synchronization
ENDDO

这里需要注意一点：处理器拥有哪些数据是由数据分布方案确定的（计算表达式的 LHS），它一般与处理器需要访问的数据（计算表达式 RHS）并不相同，每一个计算节点内部应当根据具体的需求，选择需要与之设置同步消息的 strip 。

为了便于消息生成，降低通信成本和复杂度，此处可以采用一些编译优化方案对源码进行处理：

• 消除条件执行
  • 尽量合并条件语句，以尽可能缩减迭代空间
• 消息聚合
  • 将一些小的消息合并起来
  • 为执行此优化，一个 tradeoff 是延迟消息的发送以实现更多消息的聚合
• 消息预取
  • 尽可能提前 send 操作，降低消息延迟

关于这一块的具体研究非常多！TODO 🤡

而谈到复制模式，问题会稍微复杂一些。由于复制模式中处理器内部存贮的是数据的不同版本，因此数据更新时，需要将当前版本的数据和版本信息广播给所有的处理器（假设选择所有的处理器）。此处涉及的是广播消息而非同步消息，优化的基本动机是尽量减少广播操作，尽可能只保留必要的点对点通信（广播操作的成本是很高的）。

相比单一所有者模式，它需要更多的写操作。

针对指令级并行

指令级并行（Instruction Level Parallelism，ILP）存在隐式（Implicit）和显式（Explicit）两个分类。其显隐性强调的是并行性能否为程序员所发掘。

• 隐式 ILP ：程序的指令集跟一般的串行程序相同，ILP 完全是通过硬件自动实现的（当前大多数处理器都是实现了相当一部分的隐式 ILP 功能）
  • 编译器可以通过指令重排等操作辅助隐式 ILP 的执行，帮助硬件更容易地发现指令并行性
• 显式 ILP：程序的指令集提供一些并行化特征，编译器 结合具体的特征，探测程序指令中可能的并行性
  • 与隐式 ILP 相比，减少了对长指令流水线和大量复杂的、耗能的逻辑电路的需求
  • 一些 ISA 提供的并行性：
    • VLIW（Very long instruction words, 超长指令字架构）
      • 将多条指令打包成一条超长指令字，进而使每条指令完成多个独立操作
    • EPIC（Explicitly Parallel Instruction Computing, 显式并行指令计算）
      • 在 VLIW 的基础上融合了超标量结构的一些优点而设计得到的，以期用有限的硬件开销为代价开发出更多的指令级并行

显式 ILP 的动机实际上可以总结为：传统的 RISC 系统结构没有能够充分利用编译程序所产生的许多有用信息（如关于程序运行路径的猜测信息），也没有充分利用现代编译程序强大的对程序执行过程的调度能力。显式 ILP 通过修改指令集架构，可以充分利用编译程序提供的信息和调度能力来提高指令并行度。

所以这一块讨论的编译优化技术就是提供 “信息” 和 “调度能力” 的 指令调度 优化技术。（看书，像是表调度、跟踪调度、软件流水线、分支预测之类的，当然，也要通过代码提升这类优化扩大 block 的规模，以发现更多的指令并行时机）

• 参考:
  • R. Eigenmann, Parallelizing Compilers for Multicores, Summer 2010, Purdue University