对称加密基本原理
首先介绍一些密码编码算法的基本背景。需要说明的是,所有的加密算法(将明文转换为密文的算法)都是基于 代换和置换 两个原理的。
- 代换:将明文中的每个元素映射成另一个元素
- 这里的元素指的是算法的输入分组,可以是位、字母、位组、字母组等
- 置换:将明文中的元素重新排列
对所有加密运算的基本要求是不允许信息丢失,也就是说,所有的运算都应该是 可逆 的。这个要求使得大多数的密码体制是基于乘积运算的,并且实现了多层代换和置换,因此很多时候我们都把密码体制称为乘积系统。
Feistel 密码结构
这是包括 DES 在内的许多对称分组加密算法采用的一种密码结构。
加密算法的输入是长为 位的明文分组(block)和一个密钥 。明文组会被分为 和 两部分(前后对半分),密钥 则会被推导成 个互不相同的子密钥,接下来这两半部分数据会经过 轮迭代加密(这 次处理过程都是相同的),最终拼成密文组,如下图所示。其中,第 轮迭代的输入 和 来自于上一轮迭代的输出,使用的密钥是第 个子密钥。
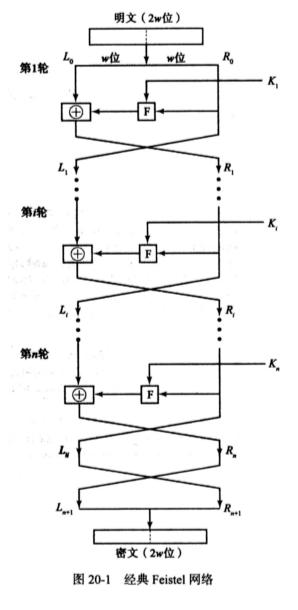
可以看到,在 Feistel 分组密码结构中,对称分组密码由一系列 轮 (round)组成,每一轮都根据一个密钥值进行代换和置换,图中的 ⊕ 符号表示异或操作(XOR),而 函数则将输入的数据半块与该轮次对应的子密钥进行处理,每一个轮次处理结束之后,需要将两个半块交换顺序,再进行下一个轮次的处理。尾部最后一次顺序交换没有密码学上的重要性,是为了在 1970s 的硬件上简化输入输出数据库的过程而设置的。
Feistel 结构的具体实现依赖于以下参数和特征:
- 分组长度
- 分组越长意味着安全性越高,但显然分组过长时会降低加解密运算的速度
- 128 位的分组长度比较合理,也能适合广泛分组密码的要求
- 密钥长度
- 特征和问题同分组长度
- 128 位的密钥长度比较合理
- 迭代轮数
- Feistel 密码采用多轮加密的本质是单轮不能够提供足够的安全性,但多轮加密可以取得很高的安全性
- 典型值是 16
- 子密钥产生算法
- 子密钥产生越复杂,密码分析越困难
- 轮函数
- 轮函数越复杂,密码分析越困难
在设计对称分组密码时,往往还需要考虑加解密算法执行速度的问题,因为很多时候它们都是被嵌入到应用程序工具中进行使用的。
同时,算法设计得太复杂的话,虽然理论上可以让它不易受到密码分析的攻击,但也增大了我们分析算法脆弱性的难度,所以在算法分析难度上也得做一些 tradeoff 。只不过,理论上这么说,实际上采用的对称分组密码都是比较难分析的,安全第一。
对称分组密码的解密本质上和加密过程一致,看成一个逆过程就好(这种可逆性是由 Feistel 结构的特性保证的)。其步骤大致为:将密文作为算法的输入,然后逆序使用子密钥进行逆运算解密(前面已经提到过密码算法需要保证可逆),即可解密得到明文。
Feistel 函数
Feistel 函数指的是 Feistel 密码结构中的 函数。下面以每个半块 32 位、每个子密钥 48 位为例介绍 Feistel 函数的步骤:
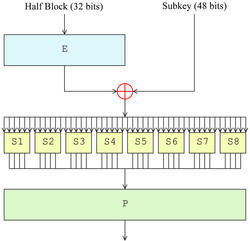
- E 扩张
- 又称扩张置换,将 32 位的半块扩展到与子密钥长度相同的 48 位,具体扩张方法是把 32 位半块分成 8 个 4 位的块,然后再用两个邻接块中紧邻的位将 4 位块填充为 6 位块
- 与密钥混合异或
- 用异或操作将扩张的结果与当前轮次的子密钥混合
- S 盒
- 与子密钥混合后,结果块被分成 8 个 6 位的块,对每个块使用 S 盒(置换盒)进行处理。S 盒使用查找表方式提供的 非线性 变换将它的 6 个输入位映射成 4 个输入位,如下图所示
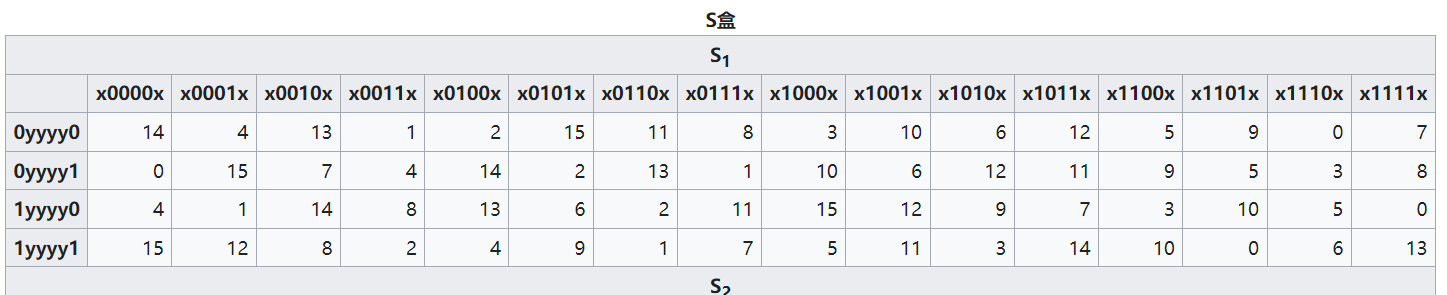
- S 盒提供了 DES 的 核心安全性 ,即非线性计算
- 与子密钥混合后,结果块被分成 8 个 6 位的块,对每个块使用 S 盒(置换盒)进行处理。S 盒使用查找表方式提供的 非线性 变换将它的 6 个输入位映射成 4 个输入位,如下图所示
- P 置换
- S 盒的 32 个输出位利用固定的置换进行重组排列,这一过程被称为 P 置换,如下图所示

- S 盒的 32 个输出位利用固定的置换进行重组排列,这一过程被称为 P 置换,如下图所示
混淆与扩散
Feistel 函数的几个步骤满足了克劳德·香农在 1940s 提出的实用密码所需的必要条件:混淆与扩散。
混淆用于掩盖明文与密文之间的关系,用来使密文和对称式加密方法中密钥的关系变得尽可能复杂。产生混淆最简单的方法是 代替 ,可以看到,Feistel 函数中的 S 盒就起到了混淆的作用。
这样看来,查找表(也即 S 盒等混淆方法)的设计对密码强度来说是非常关键的。它的设计是用来抵御密码分析攻击的,因此应当尽量让输入位和输出位之间具有较少的相关性,且输出不能由一个简单的输入函数描述出来。
扩散通过将明文冗余度分散到密文中使之分散开来,即将单个明文或密钥位的影响尽可能扩大到更多的密文中去,用来使明文和密文的关系变得尽可能复杂。意思就是,只要明文产生任何一点小更动,密文都会产生很大的差异。产生扩散最简单的方法是 置换 ,也就是换位,Feistel 函数中的 E 扩张和 P 置换都起到了扩散的作用。
密钥调度
密钥调度指的是从密钥产生子密钥的算法,下面以 64 位密钥产生 48 位子密钥为例进行说明。
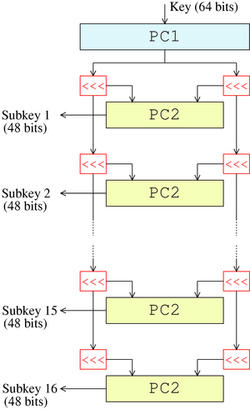
PC 是 选择置换 操作的意思。首先使用选择置换 1 从 64 位输入密钥中选出 56 位密钥,剩下的 8 位要么丢弃要么用作奇偶校验位。然后,将 56 位密钥分成两个 28 位的半密钥,在接下来的每个处理轮次中,半密钥被左移 1 或 2 位(具体数字由一个从轮次数映射到左移位数的 查找表 决定),然后通过选择置换 2 ,从 56 位密钥中选出 48 位作为子密钥。
这个选择操作并不是随机选择的,而是和 S 盒一样通过 查找表 实现。实际上,DES 中提到的很多置换操作都是基于非线性的查找表的。
在解密过程中,除了子密钥输出的顺序相反,密钥调度的过程与加密完全相同。
具体分组加密算法
需要注意的是,加密算法本身并不构成加密的实用手段,必须与某种操作模式结合才可以。操作模式的定义等已经在 密码编码工具概述 一文中有介绍。
DES
DES 结构只是 Feistel 网络结构的微小的变化。基于前面提到的 Feistel 密码结构,DES 采用 64 位的明文分组长度和 56 位的密钥长度(密钥表面上是 64 位的,但实际上只有 56 位用于实际加密,有 8 位用于奇偶校验),经过 16 轮迭代加密处理。以现在的安全标准来看,56 位密钥实在是有点短了。
3DES
3DES 使用三个 168 位的密钥执行三次 DES 算法,也即:
其中 为密文, 为明文, 表示使用密钥 对 加密的过程, 表示使用密钥 对 解密的过程。
第二步夹一个解密没有什么密码方面的含义,它的作用是让 3DES 的使用者可以解密出用单重 DES 加密的数据。不知道有没有关联,(因此)三个密钥并不一定要完全不同,FIPS 46-3 允许使用两个密钥,令 。
AES
AES 中分组长度为 128 位,密钥长度可以被指定为 128、202 或 256 位,最常见的是 128 位。不同于它的前任标准 DES ,AES 采用 代换-置换网络 (SPN)而非 Feistel 密码结构。
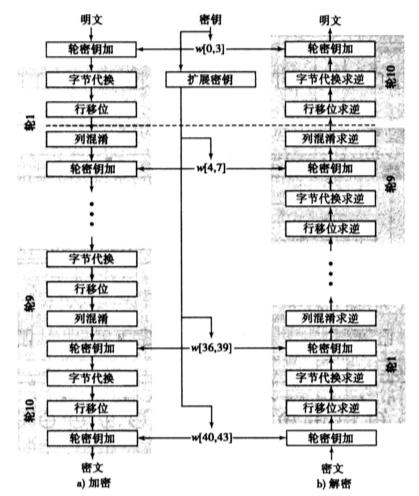
AES 会将输入明文分组分成 16 个 8 位的字节区块,由这些区块组合成一个 4 x 4 的字节矩阵,然后再这个矩阵上运作具体的加密算法。AES 也是基于轮次进行加密的,加密时,算法从一次轮密钥加开始,然后执行 9 轮迭代运算,每一轮 AES 加密循环(除最后一轮外)都包含 4 个步骤:
- 字节代换(SubstituteBytes)
- 矩阵中的各字节被一个 8 位的 S 盒查找表中对应的特定字节所替换
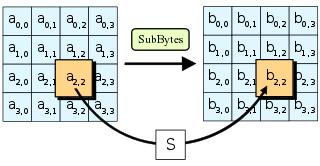
- 矩阵中的各字节被一个 8 位的 S 盒查找表中对应的特定字节所替换
- 行移位(ShiftRow)
- 矩阵中的每一行都向左循环位移某个偏移量。在 AES 中,矩阵的第 行向左循环移动 格,这样一来,矩阵中的每一竖列都由输入矩阵中的每个不同列中的元素组成
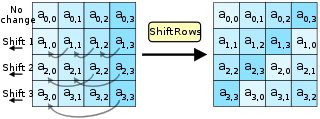
- 矩阵中的每一行都向左循环位移某个偏移量。在 AES 中,矩阵的第 行向左循环移动 格,这样一来,矩阵中的每一竖列都由输入矩阵中的每个不同列中的元素组成
- 列混淆(MixColumn)
- 矩阵中每一列的四个字节分别通过线性变换映射成一个新值,这个值是该列中所有 4 字节值的函数,具体而言,是将每一列的 4 个元素分别作为 的系数,合并成为一个多项式,然后将这个多项式和一个固定的多项式 在模 下相乘,如图所示
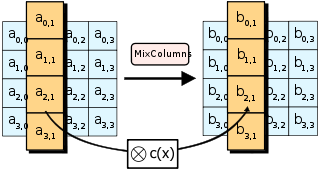
- 这一步保证了每一个输入的字节都会对输出的四个字节造成影响
- 矩阵中每一列的四个字节分别通过线性变换映射成一个新值,这个值是该列中所有 4 字节值的函数,具体而言,是将每一列的 4 个元素分别作为 的系数,合并成为一个多项式,然后将这个多项式和一个固定的多项式 在模 下相乘,如图所示
- 轮密钥加(AddRoundKey)
- 矩阵按位与该轮次的子密钥(128 位)矩阵进行列级别的异或操作
可以看到,行移位和列混淆为密码系统提供了扩散性,而字节代换则提供了混淆性。
而 AES 密钥扩展则又涉及到单独的算法。最传统的办法是将原始密钥直接复制到扩展密钥的前几个字,然后按照类似 这样的模式进行逐 字的扩展。
