Gwok HiujinGwok Hiujin

The Bird of Hermes is my name, eating my wings to make me tame.

43Archives7Categories37Tags

Jan 15, 2023NJU程序分析4429 words in 22 min

『NJU程序分析』指针分析（上下文不敏感）

与指针分析相近但不太一样的一个概念是别名分析。C Based 的经典别名分析算法（事实上都是指针分析算法，别名分析不过是其功能子集）和基本动机曾经在博文 『中端优化』别名分析与处理 - Gwok Hiujin’s Blog 中介绍过。

概述

动机

前面介绍 CHA 的时候已经讲过，CHA 只关心类的层次结构，假设经过 CHA 分析得到的调用源集合中所有的元素都来自同一类层级（比如同一个类中的不同方法），那么分析结果中就将含有大量的 false positive 样本，导致分析结果的不精确（例如，在常量传播场景下，这种情况会被定义为 NAC）。

p94sMD0.png

指针分析的动机就是在此基础上，分析出方法调用的精确指向，排除掉 false positive 。因此与快但精度低的 CHA 相比较，指针分析是一种 高精度 的过程间分析。

指针分析简介

指针分析是一种非常基础的静态分析方法，用于计算一个指针能够指向的内存位置。具体到面向对象的程序（重点是 Java），其作用则是计算一个指针（在 Java 中是变量或字段）可以指向哪些对象。

上面的叙述表明了指针分析是一种 may-analysis，因为它计算得到的事实上是指针能够指向的内存位置（在 Java 中是对象的集合）的 超近似 （也即求得的是一个指针 可能 指向的对象），这一点应当是对分析精度的 tradeoff。

这个研究领域已经有 40+ 年的历史，至今依然活跃。

Start from：William E. Weihl, “ Interprocedural Data Flow Analysis in the Presence of Pointers, Procedure Variables, and Label Variables ”. POPL 1980.

https://dl.acm.org/doi/pdf/10.1145/567446.567455

指针分析输出的结果是程序的 points-to relations。

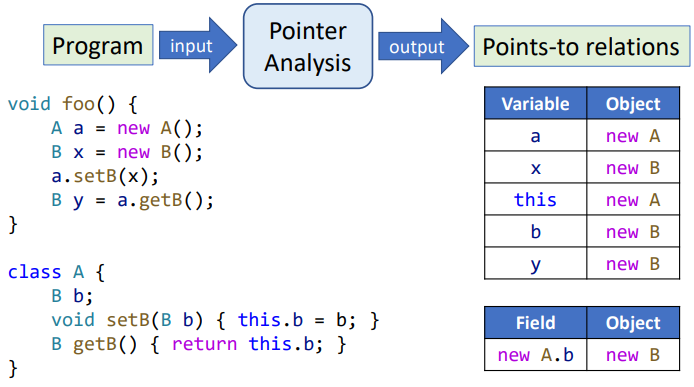
p94sQbV.png

指针分析与别名分析

文章前言中提到，有一个与指针分析非常相似但不同的概念叫别名分析。放到面向对象语言的情景下，其区别是：

  • 指针分析：一个指针可以指向哪些对象
  • 别名分析：两个指针是否指向同一个对象

别名分析的功能更像是指针分析的子集（因为显然完成了指针分析的任务后，别名分析的问题就解决了）。

指针分析的应用

  • 分析基础信息
    • 构造调用图，分析别名，……
  • 编译优化
    • 虚拟调用内联，全局值编号，……
  • Bug 检测
    • 空指针检测，……
  • 安全性分析
    • 信息流分析
  • ……

“Pointer analysis is one of the most fundamental static program analyses, on which virtually all others are built.”

——Pointer Analysis - Report from Dagstuhl Seminar 13162. 2013.

指针分析的关键因素

指针分析是一个复杂的系统，许多因素都影响着这个系统的精度和效率。下面介绍一些指针分析过程中的关键因素，每一种问题背后都有许多不同的技术选择。

Heap Abstraction：堆抽象

如何对堆内存进行建模？

  • Allocation-site：分配点抽象

在动态执行过程中，堆上的对象数量可能会由于循环或者递归的结构达到无限量级，因此对堆做抽象是必要的——否则分析算法会陷入无限循环。抽象的含义是将动态分配的、无限的具体对象建模为有限的抽象对象，以便进行静态分析。

可以看到，堆抽象的过程有点类似于将学生分成不同的班级来管理（某种聚类），相关的技术也有很多，最常用的分支是分配点抽象（Allocation-site Abstraction）。

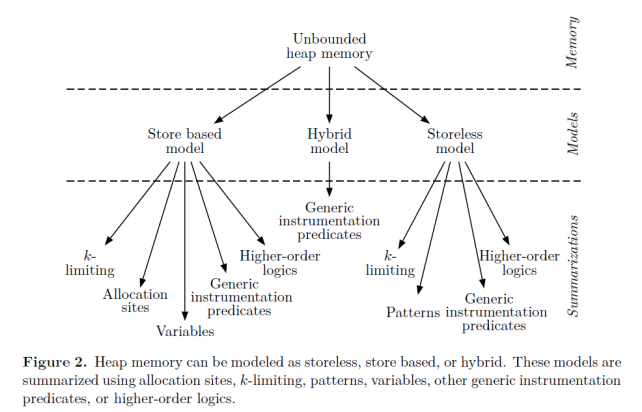
p94s1ET.png

From: Vini Kanvar, Uday P. Khedker, “ Heap Abstractions for Static Analysis ”. ACM CSUR 2016.

https://arxiv.org/pdf/1403.4910.pdf

分配点抽象的思路是将对象按照其分配点（具体到 Java 就是 new 语句）进行分类抽象，为每一个分配点建立一个抽象对象来代表其所有被分配的具体对象——毕竟一个程序中分配点的个数一定是 有限 的。

p94snvn.png

Context Sensitivity：上下文敏感

如何对调用上下文建模？

  • 上下文敏感
  • 上下文不敏感

调用上下文（calling contexts）指的是方法调用前后相关变量的值，显然参数和返回值就是上下文的一部分。在之前的博文里，也已经辨析过上下文敏感分析的含义：

上下文敏感 上下文不敏感
需要区分出一个方法的不同调用的上下文信息（关心参数等，为它们做额外的标记） 将一个方法的所有调用的上下文合并，即不做辨析
对每个方法都将分析多次（对上下文不同时的调用要做不同的分析），对每个上下文只分析一次 对每个方法只分析一次

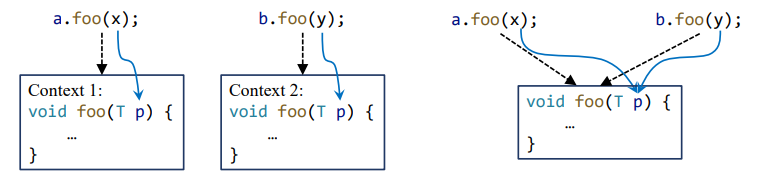
p94smgs.png

上下文不敏感的分析忽略了一部分信息，因此可能会损失分析的精度。反之，上下文敏感的分析显著提升了分析精度，是一项非常有用的技术。

Flow Sensitivity：流敏感

如何模拟程序中的控制流？

  • 流敏感
  • 流不敏感

曾经在别名分析优化的博文里详细讨论过流敏感相关的问题。流敏感分析重视语句的执行顺序，在 每个程序执行点 都分析得到了一张指示当前 points-to relations 的图；流不敏感分析则忽略了控制流顺序，将程序处理成一个无序语句的集合，分析得到的是一张面向整个程序的 points-to relations 图。显然，流敏感分析的开销是显著大于流不敏感分析的，事实上，它之于后者也并没有很大的精度优势，因此主流编译器大多数采用流不敏感分析进行优化。

Analysis Scope：分析范围

程序中的哪些部分需要被分析？

  • 整个程序
  • 需求驱动型（只分析必要的部分）

关注的语句

在指针分析中，我们只关心那些会影响到指针的语句，其他的可以忽略（比如一些控制流结构语句）。

关注的指针类型

Java 中的指针有以下几类：

  • Local variable：x

  • Static field：C.f

    • 有时也被称为全局变量（Global variable）
    • 在指针分析算法中可以当成 Local variable 进行处理，后面再谈

  • Instance field：x.f

    • 在指针分析中建模成一个具有字段 f 的对象（pointed by x）

  • Array element：array[i]

    • 处理它时我们忽略索引，将其建模为一个具有单字段的对象（pointed by array），称其为 arr —— arr 可能指向存储在 array 中的任何值。这个抽象方法在别名分析优化博文里也已经介绍过

      p94sKuq.png

因此，会影响到指针的语句就包括：

  • New：x = new T()
  • Assign：x = y
  • Store：x.f = y
  • Load：y = x.f
  • Call：r = x.k(a, …)
    • Static call：C.foo()
    • Special call：super.foo() / x.<init>() / this.privateFoo()
    • Virtual call：x.foo()
      • Which we focus

此处不必担忧形如 x.a.b.c 这样的复杂内存访问语句，因为它们在 IR 生成的初始阶段就会通过引入临时变量、生成三地址代码的方法被解析成形如 x.f 的简单形式。

理论基础

前三个部分先聚焦创建、赋值、存储、载入四种指针影响型语句，也即从过程内分析开始做起。最后一部分会引入调用语句，展开全程序指针分析。

指针分析规则

首先定义如下的表示记号，以便进行形式化定义。

内容 记号
Variables：变量 x, y \in V
Fields：字段 f, g \in F
Objects：对象 o_i, o_j \in O
Instance Fields：实例字段 o_i.f, o_j.g \in O \times F

根据这些记号，给出以下的形式定义：

指针的形式化定义

记某程序中的变量集合为 V ，字段集合为 F ，对象集合为 O ，定义这个程序中的某个指针为 p ，其中 p 满足：

p \in V \cup (O \times F)

记所有指针组成的集合为 Pointer ，则其满足：

Pointer \subseteq V \cup (O \times F)

由于指针分析的目的是输出整个程序中所有的 指向关系 ，因此根据上述定义，也可以形式化定义指向关系。

指向关系的形式化定义

记程序的指针集为 Pointer ，对象集合为 O ，其幂集记为 P(O) ，定义指向关系（Points-to Relation）是从 Pointer 到 P(O) 的映射，用 pt 表示，满足：

pt \subseteq Pointer \times P(O)

于是，我们可以用 pt(p) 表示指针 p 的 指向集合 （Points-to Set）。

规则

我们使用推导式的方式来描述各种语句在指针分析中的规则。

推导式

考虑命题 P_1, P_2, ..., P_m 和命题 Q_1, Q_2, ..., Q_n ，定义推导式（Comprehension）形式如下：

\frac{P_1, P_2, ..., P_m}{Q_1, Q_2, ..., Q_n}

其含义是，若 P_1, P_2, ..., P_m 为真，则 Q_1, Q_2, ..., Q_n 为真。其中， P_i 称为前提（Premises）， Q_j 称为结论（Conclusion）。若 m = 0 ，则称结论无条件（Unconditional）成立。

各种类型语句的规则表示如下：

New：创建语句
  • 语句： i: x = new T()
  • 规则： \frac{}{o_i \in pt(x)}

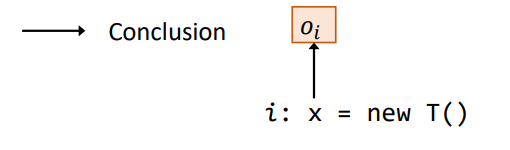
p94s3UU.png

Assign：赋值语句
  • 语句： x = y
  • 规则： \frac{o_i \in pt(y)}{o_i \in pt(x)}

p94s85F.png

Store：存储语句
  • 语句： x.f = y
  • 规则： \frac{o_i \in pt(x), o_j \in pt(y)}{o_j \in pt(o_i.f)}

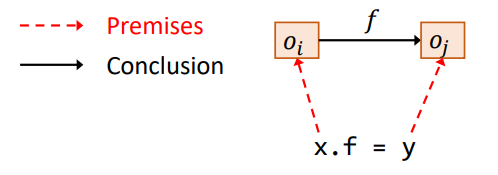
p94sJC4.png

Load：载入语句
  • 语句： y = x.f
  • 规则： \frac{o_i \in pt(x), o_j \in pt(o_i.f)}{o_j \in pt(y)}

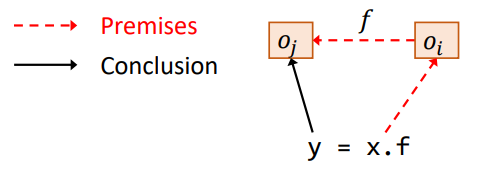
p94sY8J.png

如何实现指针分析

本质上说，指针分析的过程就是在指针（变量 & 字段）之间 传播 指向关系，这一点从指针分析规则的推导式中也可以看出。前面我们根据语句的语义确定了一系列的指向集合传播规则，因此，我们可以将指针分析的过程视为求解一个 包含约束 （inclusion constraints）系统的过程。这种分析风格被称为 安德森式分析 （Andersen-Style Analysis）。

实现指针分析的关键是：当 pt(x) 改变时，将改变的部分传递给和 x 相关的其他指针。具体的解决方案是：

  • 使用一个 图 数据结构连接相关的指针
    • 指针流图 PFG
  • 当 pt(x) 改变时，将改变的部分传递给 x 的后继

指针流图：Pointer Flow Graph（PFG）

指针流图是一个用以表示对象如何在程序中的指针之间流动的有向图。

  • 结点：PFG 中的一个结点 n 表示一个指针，即一个变量或者某个对象的字段
    • n \in Pointer
    • PFG 的结点即程序中所有的指针
  • 边：PFG 中的一条边 x → y 表示指针 x 指向的对象可能会流到指针 y 的指向集合中，即可能同时被 y 指向
    • 需要根据程序中的语句以及语句对应的指针分析规则添加 PFG 的边
      • New： N/A
      • Assign： x ← y
      • Store： o_i.f \leftarrow y
      • Load： y \leftarrow o_i.f

有了 PFG 以后，指针分析就可以通过计算 PFG 的传递闭包来解决。

分析步骤

  • 构建指针流图 PFG
  • 在 PFG 上传递指向信息

显然，这两个步骤有相互依赖的关系——构建指针流图需要指向信息，传递指向信息的时候又需要有指针流图的基础提供后继。因此指针流图是在指针分析的过程中 动态更新 的。

指针分析算法

过程内上下文不敏感的全程序指针分析算法

p94sNvR.png

Worklist

Worklist 中包含了需要被处理的指向信息 ，也即 WL \subseteq Pointer \times P(O) 。Worklist 中的每个表项 <n, pts> 表示一个指针 n 和指向集合 pts 的有序对，意味着 pts 应当被传递给 pt(n) 。

Worklist 的内部大致是这样：

[(x, \{o_i\}), (y, \{o_j, o_k\}), (o_j.f, \{o_l\}), ...]

个人感觉结合了 Worklist 的定义后主体算法就比较好理解了。

差量传播

需要注意一下计算 \Delta 实现差量传播（Differential Propagation）的部分，其动机是避免处理和传播冗余的指向信息。实际上，和已有的指向集合相比， \Delta 通常很小，所以仅仅传播新的指向信息 \Delta 能够极大地提升分析效率。

Store 和 Load 语句的指针流会受已知的指向关系的影响，新的指向关系可能会在这两种语句的作用下引入新的 PFG 边，在算法末尾的部分使用差量传播对此进行了处理。我们的 IR 都是基于三地址码的，因此我们只会通过变量访问实例域，算法末尾处的判断可以避免后续处理的冗余（如果 n 是一个实例字段，就不会存在关于 n 的 Store 和 Load 语句了）。

显然，一个 Assign 语句只会产生一个 PFG 边，而一个 Store 或者 Load 语句可能产生多个 PFG 边。

带方法调用的指针分析：全程序

全程序也即过程间的指针分析需要调用图，否则确定不了 pt(x) 的内容。此时，使用 CHA 构建的调用图是不合格的，因为基于变量的声明类型解析目标方法会引入很多虚假的调用边，进而引入虚假的指向关系。而使用指针分析，就可以根据更精确的指向关系，即 pt(x) 来解析目标方法，使得构造出的调用图更加精确。

这一段话读起来好像有点“自相矛盾”的意味，但看了前面构造 PFG 的算法后，应当敏锐地感觉到指针分析和基于指针分析构造调用图之间又是一个 相互依赖 的动态过程。我们称这种边使用调用图、边构造调用图的构建方式为即时调用图构建（On-the-fly Call Graph Construction）。

调用语句的分析规则

  • 语句： r = x.k(a1, a2, ..., an)

  • 规则：
    \frac{o_i \in pt(x), m = Dispatch(o_i, k), o_u \in pt(a_j)(1 \le j \le n), o_v \in pt(m_{ret})}{o_i \in pt(m_{this}), o_u \in pt(m_{pj})(1 \le j \le n), o_v \in pt(r)}
    其中：

    • m_{this} 指 m 方法对应的 this 变量
    • m_{pj} 指 m 方法的第 j 个形参
    • m_{ret} 指存放 m 方法返回值的变量
    • Dispatch(o_i, k) ：根据对象 o_i 的类型来做虚方法 k 的派发，从而准确地找到对应的目标方法 m
      • 该算法是 绝对精确 的 ，因为它的基础是对运行时的模拟。此处影响精度的因素只有变量 x 的指向集合内可能有不止一个指向对象

可见这条规则在 PFG 中产生的边应当是 a_1 \rightarrow m_{p1}, ..., a_n \rightarrow m_{pn}, r \leftarrow m_{ret} 。

p94st29.png

x 到 this 的那条边不能添，因为接收对象只应当流到自己 对应 目标方法的 this 变量中，唐突加上这条边会导致 x 指向集合中所有的对象都流到 this 中，产生虚假的指向关系（比如父类的对象流到子类的方法，或者子类的对象流到父类的方法）。

过程间指针分析

指针分析和调用图构建是相互依赖的，需要动态地共同进行。调用图向我们展示了一个“可达的世界（reachable world）”：

  • 入口方法（比如 main）是一开始就可达的
  • 其他的可达方法是在分析的过程中不断发现的
  • 只有可达的方法和语句才会被分析

我们称调用图中入口方法（Entry Methods）以及从入口方法可达的其他结点为可达方法。所有可达方法构成了一个 可达调用子图 （Reachable Sub-Call-Graph）。我们平时所说的调用图，事实上指的就是可达调用子图——显然，对于控制流无法到达的地方，我们并不关心，也不用去分析。

算法

过程间上下文不敏感的全程序指针分析算法

p95Zkct.png

其中 Dispatch 过程见 [『NJU程序分析』过程间分析 - Gwok Hiujin’s Blog](https://gwokhiujin.github.io/2023/01/05/『NJU 程序分析』过程间分析#method-dispatch-of-virtual-calls) 。

  • AddReachable 子过程：拓展可达调用子图
    • 添加新的可达方法和语句
    • 为新发现的语句更新 Worklist 和指针流图
    • 调用情景
      • 一开始的时候对入口方法调用
      • 当新的调用边被发现时调用
  • ProcessCall 子过程：实现调用语句的分析规则
    • 根据接收对象类型以及调用点处的方法签名做方法派发（Dispatch 过程）
    • 即时构建调用图
    • 传递参数和返回值

最好用一个简单程序在纸上推一遍，加深印象。

Buy me a cup of coffee ☕.

1 概述
1.1 动机
1.2 指针分析简介
1.2.1 指针分析与别名分析
1.2.2 指针分析的应用
1.3 指针分析的关键因素
1.3.1 Heap Abstraction：堆抽象
1.3.2 Context Sensitivity：上下文敏感
1.3.3 Flow Sensitivity：流敏感
1.3.4 Analysis Scope：分析范围
1.4 关注的语句
1.4.1 关注的指针类型
2 理论基础
2.1 指针分析规则
2.1.1 指针的形式化定义
2.1.2 指向关系的形式化定义
2.1.3 规则
3 如何实现指针分析
3.1 指针流图：Pointer Flow Graph（PFG）
3.2 分析步骤
4 指针分析算法
4.1 Worklist
4.2 差量传播
5 带方法调用的指针分析：全程序
5.1 调用语句的分析规则
5.2 过程间指针分析
5.2.1 算法