『编译优化』Instructions Scheduling: 指令调度优化

这一章之前做项目的时候因为涉及到了，所以只是简单地了解了一下算法伪代码，就直接拿去用了😱直到昨天坐高铁回家才有空静下心来读完，其中涉及到的许多调度思路都还是很有启发性的（我在做的是循环调度，了解了这一块的基础之后也更好地理解了之前看的循环优化论文与源码）。
另：需要吐槽一下的是此章节的中文翻译质量略低，看了一点之后有点看不下去，还是掏出了原版 …… 软件流水线辅助调度的部分打算之后另写，这一章里涉及的有点太浅了，而且思路不是很清晰。

指令调度的基本动机也就是通过重排指令，在不影响程序运行正确性的情况下，通过有效利用处理器资源 改进程序的运行时间 ，这一点我们已经很熟悉了。但这里的指令重排有别于代码生成步骤针对中间代码进行的指令重排，此时重排的对象是 汇编指令 —— 也就是说，此时我们假定输入的代码是 已经优化过 的，在这个步骤中我们不重复优化器的工作，而是旨在将各条指令组装到可用处理器周期和功能单元发射槽中去，本质上是试图在每个处理器周期内执行尽可能多的操作。可以认为，这个步骤属于所谓的 “后端优化” 的一环。也因此，调度器的选择显然会受数据流、指令延迟、目标处理器能力等的约束。

最简单也是我们最熟悉的一个实践例子是：将长延迟的操作（例如 load、store）与引用其结果的操作隔离开，使得不依赖其结果的操作可以与长延迟操作并发执行，起到一个 隐藏延迟 的作用。像下面这张图展示的一样：

在一般的现代处理器上，我们的目标是：

• 尽可能减少指令延迟周期数量，书中又称 “避免拖延”
  • 在计组实验中我们已经对 “拖延” 的概念有所体会：为了防止在定义一个值的操作执行完成之前读取该值，往往会对许多指令操作设置 延迟值 ，具体而言是依赖编译器添加 nop 指令，或者硬件自身提供具体的 互锁 机制，前者称为静态调度，后者称为动态调度
  • 可见，经过指令调度后，我们应该通过避免拖延或者生成 nop 指令来最小化执行时间
• 尽量避免延长值的生命周期（不要一直占着寄存器）

而针对更复杂的情况，例如允许在每个周期内发起执行多个操作的处理器（即实现了指令并行性，比如超标量处理器），我们也具有更高的优化要求，就是使尽可能多的功能单元保持忙碌状态，尽可能应用硬件的并行资源。

关于运行时间的性能量度有许多种不同方式，最常用的两种是 每秒指令数 和 benchmark 测试 （测量完成一项固定任务所需的时间）。只不过为了评估编译器后端生成代码的质量，单一度量包含的信息一般都是不够的。

编译器中用于指令调度的基础技术是基本块内的 贪婪表调度算法 ，它的思路是使用各种优先级排序方案指导汇编指令的排序，当然，也可以将表调度技术应用到更大的范围中（这就涉及更多的调度框架）。“表” 是指令调度器的输入，其内容是由目标机器汇编语言操作组成的一个有序列表，经过处理后期望得到的输出是同列表的另一个有序版本（可能还会添加一些 NOP 指令以保持代码的正确执行）。

这里还需要注意：我们知道在超长指令字架构的机器上，调度器往往会将多个操作（以操作码度量）打包为一条指令，在一个给定周期中执行，此时编译器仍需要对操作进行重排，使得处理器能够在每个周期发射尽可能多的操作。也就是说，指令调度的本质应该是 “ 操作调度 ” 。

依赖关系图

指令调度问题定义在基本块 BB 的依赖关系图（或称前趋图，precedence graph）  上。 中每个结点对应 BB 中的一条语句，它包含 操作类型 和 延迟 两个属性（因为一条语句  对应的操作必须在由其操作类型指定的功能单元上执行，而该操作需要  个周期完成，DAG 中应该包含这两个关键信息），有向边指示 BB 中值的流动。也就是说，对于两个结点  和  ，如果  使用了  的结果， 中就产生一条  的边，这就是 “前趋” 的含义。

 中不存在前趋结点的结点称为叶结点，由于叶结点不依赖于任何其他操作，它们应当被尽早调度执行；不存在根结点的结点则称为根节点，它们是最 “受限制” 的结点，因为它必须在其每个祖先之后执行。需要注意的是  不是一棵树，而是由多个 DAG 形成的森林。

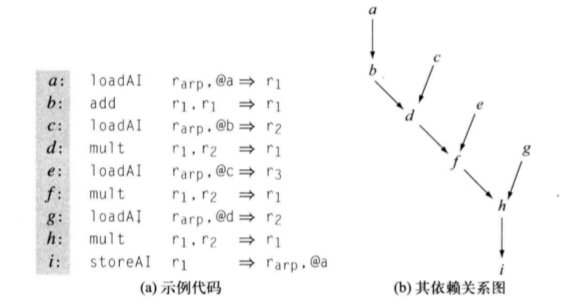
得到一个初始的依赖关系图后，调度  需要将每个结点  映射到一个非负整数  上，表示对应操作应该于哪一个周期发射，可以用一个简单的定义  来表示。根据处理器的知识我们可以知道，一个周期内可以完成多条操作的发射，也就是说针对每个周期可以维护一个操作集合  。

基于这样的数学定义，我们规定调度  必须满足以下三个约束：

• 良构性：对于每个  ，都有 
  • 含义是禁止在执行开始之前发射操作
  • 为了一致性起见，调度还必须至少有一个操作  满足  ，也就是第一个周期不可以为空
• 正确性 ：如果  ，那么 
  • 这条约束是显然的，如果  需要用到  的值作为操作数，那么在操作数完成定义之前我们肯定不能发射这条操作，因为这违反了数据流依赖关系，很可能导致错误的结果
  • 对正确性的约束强烈暗示我们：调度的基本原则是不可以破坏数据流关系
• 可行性：每个指令包含的各个类型  的操作的数目，不可以超过目标机在单周期内的发射能力
  • 这里的 “每指令” 对应的就是一个周期  ，想想 VLIW 机器的特性就可以

给出一个满足上述三种特性的调度，我们可以用以下公式得到调度的总执行时间，或者说长度（假定第一个指令在周期 1 发射）：

随着调度长度的概念，我们自然地可以引入 时间最优调度 的概念（time-optimal schedule），指示长度最小的可行调度。

某操作的总延迟可以由依赖关系图得到。前面提到过每个结点都有 延迟 属性（当然这个延迟是针对单操作而言的运行延迟），那么我们只要找到一条从叶结点到结点  的路径，将其经过结点的延迟加和，就能得到结点  的总延迟。对于一张图中延迟最长的路径，显然它决定了对应代码的总体执行时间，我们把它称为 关键路径 。

关键路径的存在可以为我们指示调度顺序。例如，假使存在许多个叶子结点，它们是调度的初始候选者，此时，选择位于关键路径上的叶子节点并将其调度到第一条指令中可以获得更大的时间收益。

指令调度与寄存器分配

前面给出的信息基本上是在用时间度量调度的质量，并以此指导调度算法，但实际情况并没有这么简单，最突出的一点可能是对寄存器资源的使用。同一 BB 产生的不同调度对寄存器的需求可能不同，寄存器分配的结果也可能改变指令调度问题。

贪婪表调度算法

从前面的内容我们知道调度的困难之处在于既要高效重排指令又要维护数据流正确性，我们必须确保每个操作只在当其操作数可用时才发射，但实际上调度器每一次对操作所属周期的选择都影响了其他操作的置放周期。除了最简单的体系结构以外，所有其他体系结构上的局部指令调度问题都是 NP完全 的。

为此编译器使用贪婪启发式算法对调度问题生成近似解，表调度就是一类最常用的启发式技术。

⭐ 局部表调度（讨论单发射机器）

前向表调度

基础的表调度运行在一个基本块内，避免了考虑分支代码序列的复杂情形。

当然跨程序块的调度也是需要考虑的，例如，一个操作数很有可能取决于位于不同程序块内的定义（这种情形影响了我们对操作数何时就绪的判断）。这里只以单 BB 的情形介绍基础算法。

它包含四个基本步骤：

• 重命名值以避免反相关
  • 一个类似 SSA 的过程，为每个 定义 分配一个唯一名字 —— 因为反相关问题一定程度上限制了调度器重排指令
  • 反相关 ：如果操作 x 位于操作 y 之前，且 y 操作中重定义了一个 x 中使用的值，则称操作 x 反相关于 y，记作  ，如果将 y 移动到 x 之前会导致 x 计算出一个不同的值
• 自底向上遍历 BB，从叶结点到根结点建立依赖关系图
  • 因此这种算法也被称为前向表调度
• 为每个操作指定优先级
  • 在每个步骤从可用操作的集合中选择时，调度器需要用操作优先级作为指引。最经典的一个优先级方案之前已经提及，就是使用从当前结点到  的根结点之间、以延迟为权重计算长度时最长路径的长度作为优先级，显然，关键路径上的结点优先级更高
• 重复选择一个操作并调度它
  • 算法从程序块的第一个周期开始，在每个周期内选择尽可能多的操作发射，接下来，周期数 + 1，算法更新已就绪可执行（操作数全部已定义）的操作的集合，并重复这些操作，调度下一个周期，直到每个操作都已经调度完成

可见关键步骤是第四步的调度算法。假设目标处理器只有一个功能单元时，调度算法的基本框架是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

Cycle <- 1
// 模拟时钟
Ready <- leaves of D
// 当前周期可执行的所有操作
Active <- []
// 在更早的周期中发射但还没有完成的操作

while (Ready ∪ Active != [])
	for each op in Active
		if S(op) + delay(op) < Cycle then
			// 说明当前周期内 op 已完成
			remove op from Active
			for each successor s of op in D
				if s is ready
					// 讨论 s 的所有操作数是否都已就绪
					then add s to Ready
		if Ready != [] then
			op = Ready.pop
			S(op) <- Cycle
			// 在一个周期内尽可能多地发射操作
			add op to Active
		Cycle <- Cycle + 1

对单个 BB 内的指令进行调度时，我们还必须对 BB 结束处的分支或者跳转指令进行调度。因此，如果  是 BB 末尾的分支指令，那么它不可能早于周期  调度执行 —— 对于单周期分支操作，它必须在 BB 的最后一个周期调度执行，而双周期分支指令必须不早于 BB 的最后第二个周期调度执行。

再观察算法，从 Ready 队列中挑选操作的机制显然决定了算法生成的调度序列的质量。当 Ready 列表在每次迭代中至多包含 1 项时，生成的必然是最优调度，而当某些周期 Ready 列表包含多个操作时，则可能出现多种不同的选择。此时算法应当选择具有 最高优先级得分 的操作，在同分的情况下，则还应该使用其他的一些条件打破平局。

打破平局的策略

为了破解同分情况下的操作选择问题，调度器的解决策略是准备很多条不同的优先级排序算法，并且依序应用这些优先级。当比较产生同分时，使用下一级优先级排序进一步比较。

除了前面给出的以延迟为权重计算的路径长度之外，还有以下优先级方案可供选择（在实践中没有孰优孰劣的固然标准，因此它们的应用顺序也没什么规定）：

• D 中直接后继结点的数目
  • 倾向于在 Ready 队列中保留尽可能多的操作
• D 中后代结点的总数
  • 放大了上一条优先级效应，这可能导致一个为其他结点计算关键值得结点尽早调度
• 结点的 delay
  • 尽早调度长延迟操作
  • 可以让余下的更多操作用于覆盖它的延迟
• 结点操作数中，最后一次被使用者的数目
  • 可以将最后一次使用移动到尽可能接近它的定义的位置，减少对寄存器的需求（缩减该操作数的生命周期）

后向表调度

表调度算法的另一种表述，顾名思义，表示从根节点到叶结点进行调度，因此第一个被调度的操作最后一个发射，最后一个被调度的操作第一个发射。

它跟前向调度比也没有孰优孰劣之分，只不过是在指令调度问题中，编译器需要利用启发式规则的不同组合运行调度器若干次，保留质量最好的调度，因此也需要考虑后向调度的表现而已。

不同调度方向的表现可能与具体程序有关。如果调度质量高度依赖于对某一小组操作的缜密排序（事实上这种情况感觉还不如手写汇编了……），若这组操作聚集在叶结点附近，那前向调度的效果可能更好，若聚集在根结点附近，则后向调度的考察可能更充分。（因为对应的反向调度都需要跨过整个 BB 才能到达这些操作，如果有其他操作可以在同一个周期内被填充，调度器就暂时看不到它们，此时前向和后向的结果可能就差了几个周期）

平衡调度：调度具有可变延迟的操作

表调度算法高效执行的一个重要基础是对  的精确估计，然而实际上我们很难做到这一点，尤其是针对内存操作（load 和 store 等）—— 在具有多级 Cache 的机器上，load 操作的实际延迟可以是 0 个周期也可能是数百数千个周期，贸然地将该操作的延迟假定为最坏情形、最好情形或者平均值都很不合适。针对此类具有可变延迟的内存操作，我们需要额外使用一些算法尽可能准确地估计它们的  值，对应的策略被称为平衡调度。

此时编译器采用的策略是根据可用于掩盖 load 操作延迟的指令级并行性的数量，为每个 load 操作单独计算相应的延迟。直白地说，就是计算代码中那些可能与 load 并行执行（也即与它无关）的操作数量，用它们的总延迟来度量 load 的可能延迟。这一思想的精妙之处在于把程序中的局部并行性分发到了各个内存操作上，反过来还能为每个 load 尽可能多地调度可用的延迟。

在依赖关系图上，平衡调度是很好实现的。下面给出算法伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

for each load operation l in the BB:
	delay(l) <- 1
	// 1. 初始化
	
for each operation i in D:
	let D[i] be the nodes and edges in D independent of i
	// 2. 找到 D 中与 i 无关的所有计算
	for each connected component C of D[i] do
		// 3. 查找 D[i] 的连通分量 C 中所有路径上的 load 操作
		find the maximal number of loads, N, on any path through C
		// 说明 C 中最多有 N 个 load 操作可以共享独立操作 i 的延迟
		for each load operation l in C:
			// 4. 将各个独立操作富余的延迟平均分配给可并行执行的 load 操作
			delay(l) <- delay(l) + delay(i) / N

第二步可以抽象成一个图可达问题，D 中所有与 i 不可达的点和边构成的集合就是 D[i] 。

提高表调度效率

主要是一些数据结构上的优化。例如：

• 从 Ready 列表中选择操作的线性扫描过程使得创建和维护 Ready 的代价接近  ，此时将列表替换为优先队列可以把操纵 Ready 的代价降低到 
  • 类似的优化可以应用到 Active 列表上
• 调度器可以维护一组独立的 Worklist 列表，每个列表对应于一个周期，包含将在该周期内完成各个操作，空间换时间来避免搜索 Active 的  代价
• ……

讨论多发射机器的表调度算法

前面为了便于说明算法，假定每个周期只能发射一个操作，但我们都知道大多数处理器一个周期可以发射多个操作。此时，在算法的 while 循环内，我们就要在每个周期内为每个功能单元都分别寻找一个可发射的操作。

显然需要进行的扩展是增加遍历功能单元的循环，并且优先调度限制较多的功能单元（因为有些操作没法在多个功能单元中执行）。

区域性调度：扩展表调度范围

之前谈区域优化的时候已经知道，“区域性” 强调的是大于单个 BB 但小于整个过程的区域（也就是扩展基本程序块 EBB ），类似值编号技术，从单个 BB 移动到较大范围当然可以改进生成代码的质量。区域性调度算法的引擎也是前面提到的表调度算法，只不过是改变了应用表调度的上下文环境而已。

EBB 调度：基于扩展基本程序块的调度

为了使表调度获得更大的上下文环境，我们将表调度的范围从 BB 扩展到 EBB —— 具体而言是利用了 EBB 树形结构的 “超局部” 而不是泛化的 “局部” ，这一将线性 EBB 作为单个 BB 考虑的处理思路在局部值编号技术中已经学习过。但在表调度中，超局部思维带来的两个问题可能使得表调度复杂化：

• 共享路径前缀
• 过早退出

用一个例子说明。针对下面这张 CFG ，我们知道可以将 <B1, B2, B4> 和 <B1, B3> 这两个 EBB 分别作为单个 BB 处理：

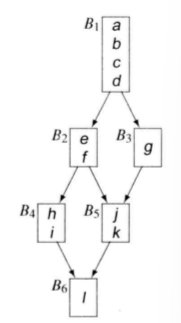
共享前缀可能带来的问题是：

🔦假使将 <B1, B2, B4> 作为一个 BB 考虑，调度时将指令 a 移动到了 B2 中，这一调度可能加速了 <B1, B2, B4> 这条路径的执行，但却可能改变沿 <B1, B3> 路径的计算 —— g 还有可能用到 a 呢！此时，调度器必须使用 插入补偿代码 的方法来解决问题。

补偿代码：指插入到程序块 B 中，用以抵消不含 B 的代码路径上跨程序块的代码移动所带来的副效应的代码。

假设 g 确实要使用 a，那么此时需要在 B3 中插入一份 a 的副本作为补偿代码。这一举动不会延长路径 <B1, B3> 的执行，但是增加了代码片段的总长度。

类似的问题同样会出现在过早退出上，因为过早退出的本质是某一个线性的 EBB 路径内实际包含分支的一部分，对于分支的另一部分（如图中的 B5），它与另一条分支共享的、位于线性 EBB 内的共享前缀会带来相同的问题。

🔦假使将 <B1, B2, B4> 作为一个 BB 考虑，调度时将指令 f 前提到了 B1 中，这一操作的后果是为 <B1, B3> 路径带来了一个额外操作，延长了该条路径的执行时间，甚至还有可能产生不正确的代码。（此时需要应用活跃变量分析辅助判断）

此时为了抵消 f 带来的副作用，编译器需要在 <B1, B3> 路径上的每一个 BB 中重写代码，可能要插入很多条补偿操作 —— 这会进一步降低沿路径 <B1, B3> 的执行速度。

为了减少补偿代码带来的影响，我们往往需要使用数据流分析信息约束 EBB 调度中的指令重排行为，最常用的就是活跃变量分析。在这种方案中，表调度的步骤被修改为：

• 在区域内执行重命名
• 分析得到区域内的线性 EBB 路径，对整条路径建立单一的依赖关系图，此时忽略了任何过早退出的情况
  • 此时，编译器调度每个 “BB” 一次（将合法线性 EBB 处理成一个 BB ），隐含处理了共享前缀问题。以上面的例子为例，调度器分别会处理路径 <B1, B2, B4> 和 <B1, B3> ，处理完 <B1, B2, B4> 后，由于 B1 的调度已经固定，此时会将它的调度知识作为处理 B3 的初始条件
  • 这指示我们选择优先级排序的时候，应当优先调度那些 “热” 的块，也就是执行最频繁、最有可能成为公共前缀的基本块（基于数据流分析结果判断），而后才考虑较 “冷” 的块
• 在依赖关系图上应用表调度算法，每次调度器将一个操作指派到调度中一个具体周期的具体指令中时，需要遵守活跃变量信息约束，并插入任何必要的补偿代码

⭐ 跟踪调度 Trace Scheduling

为超长指令字架构开发。针对这种体系结构，编译器的动机是使尽可能多的功能单元处于忙碌状态。

跟踪调度进一步扩大了调度范围，不再专注于 EBB 路径，而是试图构造穿越全程序 CFG 的最大长度无环路径（称为 “踪迹” ，Trace），将表调度算法应用到这些踪迹上。

选择路径的标准是所谓的 “剖析信息” 。“剖析信息” 是指编译器在代码编译过程中生成的用于分析程序性能的信息，这些信息可以包括代码的执行时间、函数调用次数、内存使用情况等。剖析信息可以帮助开发人员了解程序的性能瓶颈，找出需要优化的部分，并提供优化建议。在调度过程中，编译器可以根据剖析信息来优化代码的执行顺序、并行化处理等，以提高程序的性能。

建立可供调度的踪迹时，最常用的剖析信息是 CFG 中各条边的执行次数，用贪婪的方法，在每次遇到分支时选择执行次数最多的边加入踪迹，最终贯穿整个原始 CFG。需要注意的是，踪迹的构造会在遇到循环控制分支指令时停止，然后从循环的末尾重新开始 —— 这是为了防止调度将代码移出循环造成错误。

将表调度应用于踪迹的过程跟 EBB 调度是类似的，但踪迹与 EBB 的不同点在于可能存在 “中间入口” 。EBB 内部是线性的，但踪迹的中部可能存在具有多个前趋的结点，且它的部分前趋显然不可能包含在踪迹中。此时需要对这种结点做特殊处理，我们称其存在 “中间入口点” 。

假设结点  所在的踪迹存在中间入口点，不管调度需要对其进行前向或后向移动，都可能引入命名问题，因为操作的移动 可能 重定义一个 跨越 了中间入口点的变量活跃范围，影响中间入口点对应前趋程序块传递的值。此时当然要在踪迹外添加  对应的补偿代码，当然也可以添加一些调度约束，例如不准前向移动操作跨越中间入口点程序块。

最后需要提醒的一点是，类似 EBB 调度的思路，跟踪调度也是将一条踪迹处理成了一个 “BB” ，并在实际调度中会对每个 “BB” 调度一次，将前一次调度的结果作为本次调度的先验知识。

这样看来，其实 EBB 调度本质上是跟踪调度的一种 退化 情形，也就是禁止了中间入口点的跟踪调度。

超级块复制 Cloning

复制的基本动机是为了解决 CFG 中数据流汇合点（也就是存在多个前趋的结点）给跟踪调度（以及 EBB 调度）带来的限制，做法也很简单，只要把汇合点分别复制一份给它的前趋就可以了。

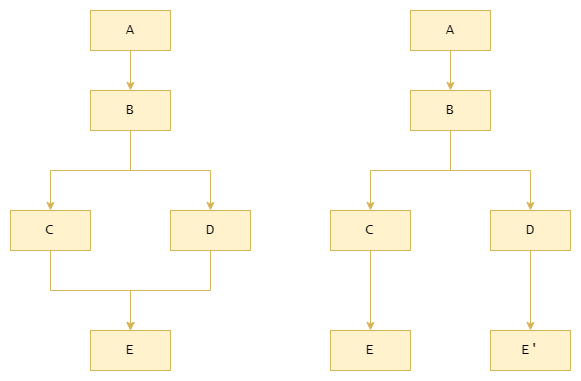
复制消除汇合点后可以扩大 EBB 或者说踪迹的范围。而且由于反复强调过的 “先验知识” 的调度思路，在实施过复制的 CFG 中，因为复制多出来的那几种选择不会彼此干扰。

复制之后编译器还可以对单纯线性的程序块对（通过一条边链接，源程序块没有其他后继，目标程序块没有其他前趋）进行进一步合并，就像我们在中端优化中做的那样。

复制还可以将尾递归优化为一个只包含单个 BB 的循环体，可以借助循环优化之类的局部方法揭示更多优化时机。

参考：

• Engineer a Compiler, Second Edition

豆瓣评论：“Keith Cooper人非常好，书也写得不错，酷爱穿花衬衫。”