参考 paper 汇总:
ANDROMEDA: accurate and scalable security analysis of web applications
Precise Interprocedural Dataflow Analysis via Graph Reachability
- 这一篇主要是 IFDS 分析的算法基础(来自 1994 年的古早文章),结合程序分析课程笔记食用当作复习 IFDS 了。
初识 IFDS 框架是在程序分析课程上,当时讲到,由于 IFDS 框架的 Distributive 特性,我们无法在此之下完成 non-distributive 的指针分析。主要是因为我们没法通过考虑每一条独立的输入边并联立独立的分析结果得出整体的正确分析结果(即不满足 的特性:如果你需要将所有 的信息组合起来才能在 中得到准确的数据流事实,那么这个分析就是 non-distributive 的)。我将此处指针分析存在的矛盾理解为精确指针信息对别名信息的依赖。当时我想当然地认为,基于指针分析的污点分析也没法通过 IFDS 框架来完成。

这位老哥完全问出了我初学时想问的,评论区解释得也非常到位。
但事实与我想的大相径庭,IFDS 框架简洁的基于图可达性的分析思想在污点分析乃至一些角度特殊的 Java 指针分析上依旧有自己强大的用武之地。
-
有一些论文扩展了原始的 IFDS 算法,使其能够给出更精确的分析;
-
既然主要的障碍在别名信息的必要性,那么如果 抛去别名信息 ,只关注 fact 的传播,我们就可以利用 IFDS 框架简化分析了——从这个动机出发,就很容易想到污点分析(Taint Analysis)。因此,有一些论文提出了 IFDS 框架下的污点分析办法,它们是基于扩展 IFDS 的;
-
有一些论文提出了使用 IFDS 进行对象敏感的指针分析;
-
……
扩展 IFDS
其实之前在程序分析课上已经了解并模拟过传统 IFDS 的示例了,扩展 IFDS 只是在那个基础上做了一些不算大的改动。

其中:
计算所有的过程内边
当 是一个 call site 时, 计算所有从此出发的 call-to-start 边
当 是一个过程的出口结点时, 计算所有从此出发的 exit-to-return 边
当 是一个 call site 时, 计算所有从此出发的 call-to-return 边
维护的是一个结点集合,这些结点应当在当前分析中已知可达当前程序点,且是当前程序点的前驱。它的作用是便于我们做流方程的 反向 处理,因为后面有一些改动要求我们做反向的追溯,比如追溯一个过程的 都由哪些调用点指向。
- 请注意
line14和line15.1的处理扩展 主要体现在以下几个方面:
-
在 exploded supergraph 上做 lazy computation ,通过确保只构建爆炸图相关的部分来减少分析的内存占用
-
支持 SSA 形式中的 结点 。控制流图中 merge points 处的 结点导致了数据流分析的精度损失,因此扩展 IFDS 算法会将数据流的 merge 操作延迟到 结点处理完之后——也即先对当前结点运用一个专门针对 的流函数 ,再将计算得到的 中的元素 merge 起来,而非 merge 它的输入。
下图中 type analysis 的例子形象地展示了 结点对分析精度的损害(图 © 是先 merge 再生成 指令的)。
b 图中,cast 操作符会 kill 掉 fact <x, Circle> (因为 Circle 不能 cast 成 Square,走左边的话都到不了 draw ),因此在 x.draw() 处唯一可能可行的类型是 Triangle,这个分析结果是精确的;
而在 c 图中,SSA 形式导致 Circle 的信息从右边被错误地保留了。传统的 IFDS 算法会首先将两个分支输出的 facts merge 起来,然后对 merge 的结点施加流方程,将 建模成 的副本,进而让错误的 Circle 信息影响了 处的分析精度。
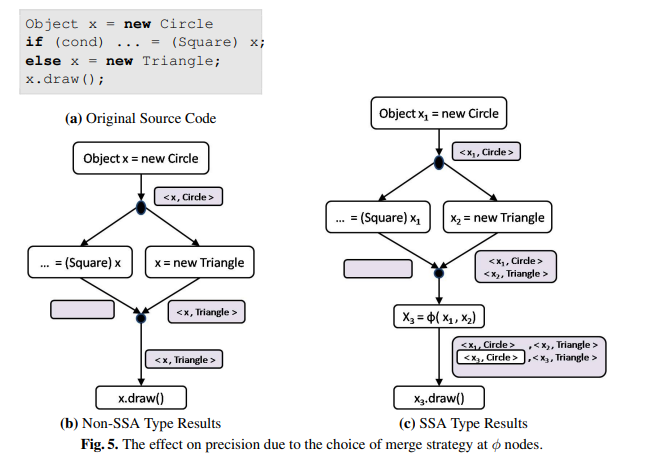
扩展 IFDS 在这里做出的改动是:
-
将所有加入到 PathEdge 中的路径与一个控制流前驱结点联系起来,写作 ,其中 指的是该条路径上的倒数第二个结点。这样一来我们可以区分控制流前驱不同但起始点和终止点相同的两条路径,譬如上图中从 到 的两条边。
- 一个优化思路是只对形如 的边添加这样的信息,毕竟 只会出现在过程的开头
-
为流方程多扩展一个参数,记录上一条谈到的控制流前驱结点,体现在算法中是
line34处的 。这样一来, 指令的流函数就可以依赖于与到达 点处的数据流值 相关的控制流前驱 。- 结合上一条改动,相当于往前z偷看了一个前驱来补充每个数据流 fact 到达的控制流边的信息。以上面那张 type analysis 的图为例,这样可以保证只有来自右边的 产生新的 fact ,避免了错误的 Circle 信息的产生。
-
-
在 返回流函数 中提供调用方状态的信息,进而允许被调用方的状态能够更精确地被映射到调用方的上下文中
-
在原始 IFDS 算法中,返回流函数由一条从被调用过程出口结点处指向 return-site 处的过程间边建模!
-
这一点乍一读起来有点抽象,下面借助一个例子来说明。
1
2
3
4
5
6void ensureCircle(Shape y) {
Shape z = y;
(Circle) z;
}
Shape x = ...;
ensureCircle(x);在 callee 中,每一个数据流 fact 都被 callee 内部的局部作用域表示,而对于很多分析来说,将 callee 内部的信息映射回调用方是很重要的,否则会造成分析图中的 断点 (本应通过调用关系传播下去的污点无法继续)。
以上面的代码为例,假使现在的分析是基于类型的污点分析,在
ensureCircle函数内部的 cast 只有在被z指向的对象(同时,该对象也应当被 x 和 y 指向)的类型是Circle或者其子类时才能成立,如果ensureCircle函数能正常返回,那么x就不应该指向一个任意的Shape,而是只能指向Circle。然而,在传统 IFDS 框架下,exploded supergraph 中并不存在一条从 callee 中的z指向 调用方 中的x的边,z指向Circle类型这个事实在ensureCircle方法的出口处就已经停止传播了。原始 IFDS 发现的 fact 需要扩展的 fact <call site, <>> [Entry, <>] ← <call site, <>> [Entry, <>] ← <call site, <>> [Exit, <>] ← [Entry, <>] 因此我们需要做的扩展,就是将被调用过程入口处参数携带的调用方上下文信息和过程间信息结合起来。具体体现在这里: 
可以看到,对于每一条 exit-to-return 边,我们通过下面那个
Propagate,沿着返回流函数成功地把被调用过程内的上下文信息(体现为 )映射到了调用点处( 集合帮我们维护了前驱,从其中遍历即可)。
-
基于 Access Path:IFDS 与精确污点分析
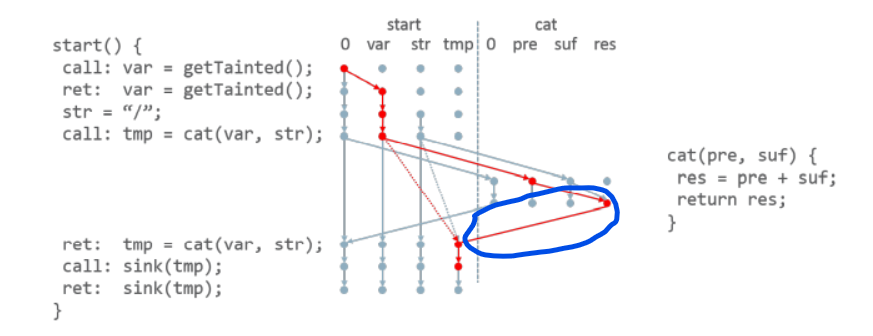
先不谈具体的分析规则,污点分析直觉上比起指针分析就更像一种所谓的污点信息 到达性 分析,污点从某一个程序点开始传播,分析的本质则是辨别污点源处的信息能否到达我们需要的程序点处,因此将其转化为图可达性问题应当可行。实际上,IFDS 数据流框架已经是 Java 应用实践中最成功的污点分析工具之一。
目前最先进的一批污点分析方法采用的是使用 Access Path 概念对 Java 程序中的对象和字段进行抽象建模,这样一来可以将污点标记的到达问题转换为图中特定节点的可达性问题。下图是一个 IFDS 框架下简单的污点分析示例图。
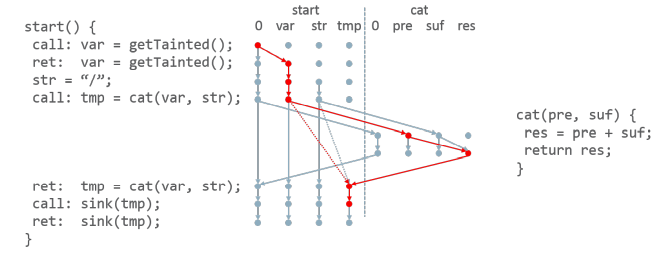
当然,这样一来污点分析算法的功能就变得很单一了,至少没有办法完整分析出程序中所有的别名信息,如有需要就得 额外再进行别名分析 。体现在具体的 IFDS Based 污点分析算法中,就是所谓的按需别名分析(On-demand alias analysis)。
IFDS 分析算法有前向和后向两种分析思路。
前向分析从污点源开始在程序中传播 tainted facts,计算全程序每一个程序点处的数据流 fact ,最终检测目标程序点处是否存在该 fact;后向分析则是需求驱动型的,从目标程序点处分析数据流 fact 能否到达污点源,得到的分析结果是 start points 的集合。对于污点分析应用,一般来说针对中型应用(对少于 100K 行的代码,分析时间最多不超过 1 小时)惯于使用前向分析,处理大型应用(多于 1M 行代码)则习惯使用后向分析加速。
背景与建模
-
一般来说用于分析的中间代码需要是 SSA 形式的
-
一定程度上保证了 distributive 特性
-
对 SSA 形式的中间代码进行分析有可能会损失分析精度(这一问题通过扩展原始 IFDS 算法可以得到解决,上文已经介绍),但它可以进一步提升别名集分析等分析的运行时间和空间水平
-
-
⭐
Access Path建模-
目前来看效果比较好的精确 IFDS 污点分析的共同思想核心
-
动机:为了精确地使用 IFDS 框架,面对诸多高级语言特性时单单使用变量名标记结点是不合适的,因此我们使用
Access Path这个概念对程序中的变量和字段进行建模 -
基本形式是 ,其中 表示局部变量或者一个参数, 表示字段。 表示首先在当前作用域中解引用 ,然后从堆中解引用字段 和 ,从而检索到的值
-
显然在真实程序中,
Access Paths是无界的,因此我们一般会使用一个 k-limit 将它们的长度绑定到预定义的长度 k 上。当访问路径的长度达到 k 时,进一步的字段追加将被简单地忽略(即超过 k 的访问路径被假定为未污染,这是一个很常见的优化思路)-
k = 0 表示一个单一的变量或参数,比如
-
一般来说 k = 5 比较合适
-
-
Access Path隐式地描述了通过这条路径可到达的所有对象的集合,例如, 包括污点 、、 等等 -
为了支持
Access Path的精确性,一般在进行 IFDS 污点分析的同时会进行按需的别名分析,即遇到算法认为需要处理的字段或赋值语句时启动一个反向的别名分析,对别名分析得到的结果都做污点传播,直到找到不动点
-
-
-
基于 扩展 IFDS 算法 进行的前向分析或者后向分析传播方程(meet & Join)
-
基础分析思路
-
赋值语句
-
对于一条赋值语句的传递函数,如果右边的操作数有一个被污染了,左边的操作数就会被污染
-
对数组元素的赋值保守处理,即认为污染了整个数组
-
将
new表达式赋值给变量 会删除所有由从 出发的access paths所建模的污点
-
-
方法调用
-
通过将实际的访问路径替换为形式参数,将
access paths转换为调用者的上下文信息(前面那张简单示例图里有体现);方法返回时将信息反向转换为access paths,其中包括方法返回值(如果存在)- 这一步操作的支持就是前面对 IFDS 算法的第三步改写
-
需要具有一个 call-to-return 流函数,在调用点和返回点之间传播与调用无关的污点
-
-
具体算法
基于上面提到的背景,使用 IFDS 框架进行污点分析就变得比较方便了,具体的方法各有不同,但效果好的那些都离不开基于 Access Path 的流方程设计。有采用后向分析的,也有采用前向分析的。如下图所示的来自 Oracle Labs 的一篇文章 IFDS Taint Analysis with Access Paths 就介绍了一种简洁的过程内后向分析算法(采用了 k-limit,限制 k = 5):

更复杂但更加精妙的则有以下这些(都比较长(意思是没认真读 🙇),有空可能会写写,论文链接都在文章开头):
-
TAJ:使用一种称为
thin slicing的方法对 JEE Web 应用程序进行污点分析-
在 thin slicing 中,IFDS 算法用于流敏感的对局部变量污染流的推理,而针对那些会通过堆的流,则通过流不敏感的预先计算好的指向信息进行处理
-
采用的是前向传播
-
在分析时使用了各种启发式方法限制分析的运行时和内存使用水平
-
-
⭐ ANDROMEDA :提出
Access Path建模思想的元祖,通过基于 IFDS 的设置计算 JEE Web 应用程序的别名和污点分析-
被污染的
Access Paths前向传播,从程序的入口点处传播到安全敏感的 sinks 处 -
按需计算别名,即在前向分析遇到字段赋值时启动反向的别名分析,然后前向分析再通过新发现的别名进一步做污点传播,以此类推,直到到达不动点
- 基于此才提出了 k-limiting 机制
-
-
⭐ FlowDroid :将 Andromeda 的数据流方程进一步融入到 IFDS 框架中,通过共享污点分析和别名分析的信息,提高了分析的精度
-
实际上,在 FlowDroid 中,只有在原始的
access paths被污染后,别名才被污染,在论文中这是一种被称为“激活语句”(activation statement)的机制 -
包括对 Android 特定框架结构的支持,这些结构很难进行静态分析
-
使用前向污点分析与按需的后向别名分析相结合的分析方法
-
使用 k - limit(k = 5)
-
