实在想吐槽一下，最近的调研实在是太难了，有效资源特别少，同时悲哀地感受到了自己的洋文水平正在急速退步……对不起 Prof Xiaodou。

有很多地方把 GCM 译作“全局代码提升”，我也就套用这个译名了，其实它的行为更接近于“提取”。首先，我们需要解释一下这个优化算法的动机。

随意地给出如下的一段代码作为例子：

1
2
3
4
5
6
7
8

public static int foo(int val) {
    int r = 0;
    if (val > 100) {
        int q = val * 3;
        r = 145 + q;
    }
    return r + val;
}

然后，我们可以直接地解析出如下图所示的 IR（有点像 ANTLR 解析出的抽象语法树，不过它其实是一般的前端方法都能解析出的 IR 结点图，是一个非常 raw 的状态）。

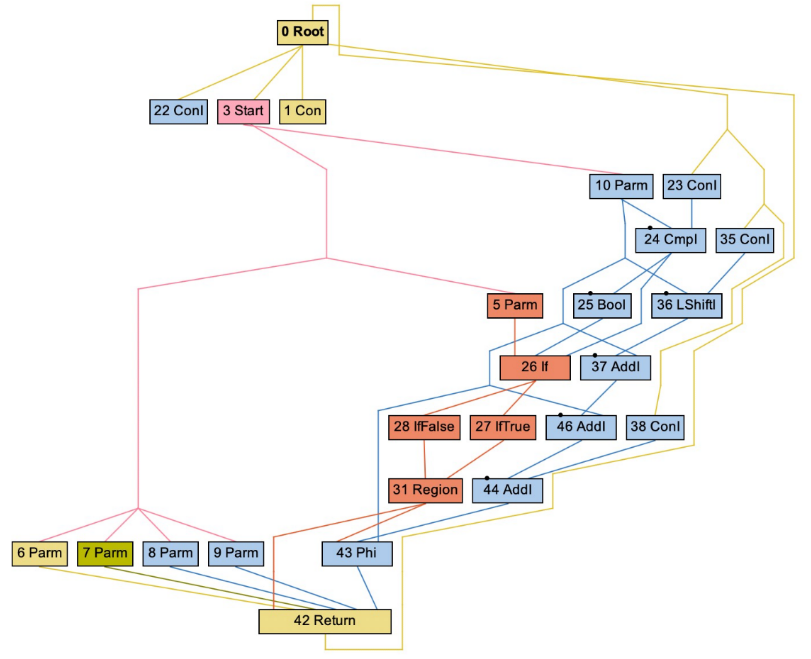
这种 IR 结点图被称为 Ideal Graph，或者“sea of node”，因为这些结点就如漂浮在海洋中一样杂乱，对于大多数指令结点，它们现在处于的基本块都是由源程序直译出来的，现在它们的控制依赖关系体现出来的控制流图结构并不是最佳的，甚至因为前面执行过的某些优化（比如全局值编号）可能还是错的。我们需要一种方式，将结点的海洋重建成我们需要的 CFG，它应当是正确的（体现在基本块中的每个指令的每个操作数都能够支配当前基本块），同时是高效的（体现在每个指令所位处的循环嵌套深度最浅），这种方法就是全局代码提升。

重建 CFG 的好处倒是显然的，毕竟它是许多优化算法的结构基础。对于我们的编译器，由于前端解析的时候构造过 Module 的基本块结构，因此完成这个结点归位的工作倒不是什么难事。

Cliff Click 给出了一个直接的近线性时间算法来完成全局代码移动 (GCM) ，算法将代码从循环中提取出来，并将其插入更依赖于控制的 (同时，可能执行频率更低) 基本块中。GCM 不是最优的，因为它很有可能会延长一些路径。它会使依赖于控制的代码脱离循环，因此如果循环至少执行一次，那么这种算法就是有利可图的。GCM 只依赖于指令之间的依赖关系（因为是基于支配树的），在执行算法时，原始的调度顺序将被忽略。

GCM 会移动指令，但它不改变控制流图 (CFG) ，也不删除冗余代码。GCM 受益于 CFG 整形(如分离控制相关的边，或插入循环的 landing pads)。GCM 允许我们为全局值编码 (GVN) 使用一种简单的基于哈希的技术，因此 GCM 和 GVN 优化往往是同时进行的。

全局代码提升（Global Code Motion，GCM）

全局代码提升算法的功能是调度那些“浮动”的指令，把它们归位到一个个基本块中，以构建成 CFG。这个过程必须保留已有的控制依赖和数据依赖。在这个大前提下，算法可以自由发挥，我们的目标就是尽可能把代码移动到循环外面，尽可能让代码的执行路径变少。它的执行步骤大致如下所示：

1. 根据 Ideal Graph 构建支配树，并用支配树深度来标注基本块。
2. 查找循环并计算每个基本块的循环嵌套深度。
3. 根据现有的控制和数据依赖关系调度指令，讨论指令能放到的最前的基本块，也就是这些指令最早被它们的输入支配的块。显然，为了寻找一个尽可能早的符合条件的基本块，这个调度方法将会产生很多生命周期非常长的预测代码。
4. 讨论指令能放到的最后的块，一般来说是最后一个它们能支配所有自己的 uses 的那个块。
5. 在上面两步中得到的最前和最后两个块之间，我们得到一个安全的放置指令的范围。在这个范围内，我们选择处于尽可能浅的循环嵌套深度中、尽可能依赖于控制的块作为最终放置指令的块。

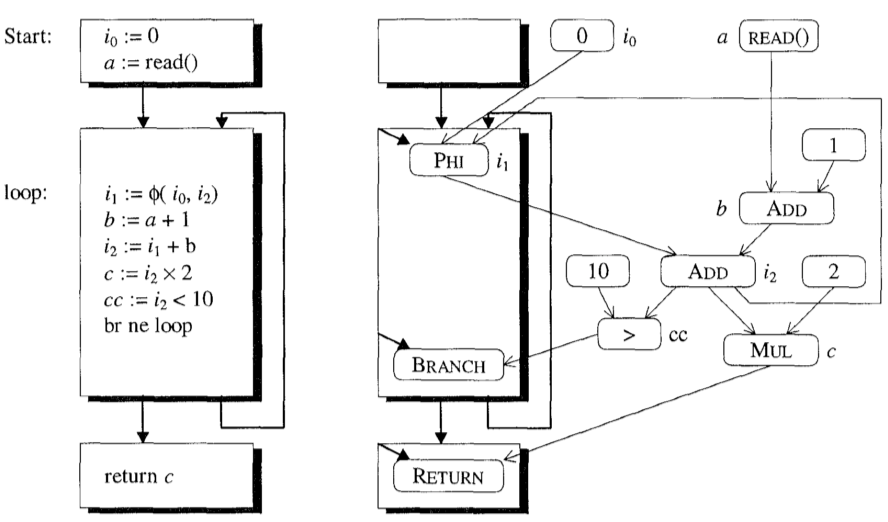
我们将在下面的小节中详细讨论这些步骤，并使用下图中的循环作为示例。左边的代码是原始程序。右边是结果图，阴影框是基本块，圆角框是指令，黑线表示控制流边缘，细线表示数据流（数据依赖）边缘。

根据 Ideal Graph 构建支配树

这里，我们需要使用到经典的 Lengauer & Tarjan 算法，这个算法有接近线性的复杂度，运行时间几乎跟 CFG 的大小成正比，但是不是很容易理解，相比之下，另外一种迭代数据流分析的方法更容易理解，只不过复杂度有 ，几乎现在所有编译方面的书籍都是介绍的这种方法。《Engineering a Compiler》的作者 Cooper 还提出了一种算法，该算法在复杂度以及实现难度上作了很好的折中，并且作者声称该算法在实际的 CFG 上的效果与经典的 Lengauer-Tarjan algorithm 相差并不多，只不过我没有去尝试。

有关支配树构建的内容，这篇博客写得非常详尽，包括理论背景、算法解析等等，可供参考：构造Dominator Tree 以及 Dominator Frontier

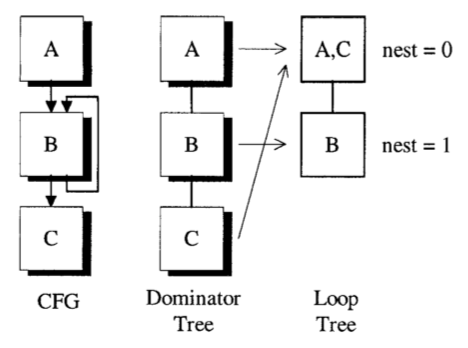
得到支配树后，我们同时得到了循环嵌套深度。这两个信息使我们能够处理基本块的预期执行时间，接下来，我们会使用这些信息来决定在哪里放置指令。根据示例得到的 CFG、支配树和循环树如下图所示，nest 指示的是循环嵌套深度：

讨论最前块

首先要进行的指令调度是讨论指令能够放置的最前的基本程序块，这是一个“贪心”式的思路（greedily），主要的动机是尽量把指令移出循环，并且缩短代码的长度。指令能够放置的最前的块是它们第一个会被自己的输入所支配的块，唯一的例外是由于某些控制依赖被“固定”（pinned）到特定块中的指令，它们包括 phi 指令、branch / jump、stop / return 指令，可以看到都是一些具有结束性质的特定的指令，因此也要放到那种特定的块里（这些块也被 pin 了），比如经典的 ret block。还有一个特殊的点是故障指令（faulting instructions），它们有一个显式的控制输入，因此它们不能被移动到自己位处的原始基本块之前，否则会导致故障的判断出现问题。

这个调度模式将会产生很多预测性质的、生命周期非常长的代码。

具体的算法流程如下所示：

从已经有控制依赖的指令（pinned，后称固定指令）开始，我们对输入做一个后序 DFS。在调度完固定指令的所有输入之后，我们再来调度指令本身。我们将指令放置在与它位处最深的支配树深度输入相同的块中。如果此时所有的输入定义都能支配指令的 uses，那么这个块就是正确的“最前块”。

但还有一个问题：我们很容易（或者说，实践中本来就经常出现）就可以写出一个输入并不支配所有 uses 的程序。考虑下面这样一段代码：

1
2
3
4
5
6
7
8
9

int first := TRUE, x, sum0 := 0;	[1]
while (pred()) {	[2]
	sum1 := phi(sum0, sum2);	[2.1]
	if (first) {	[3]
		first := FALSE;	[4]
		x := ...;	[4.1]
	}
	sum2 := sum1 + x;	[5]
}

根据这段代码，可以构造下图中右图这样的支配树，同时，我们在左图给出正确的 CFG：

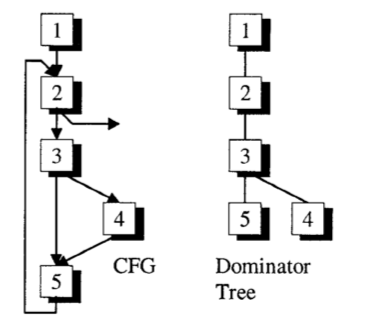
可以看到，在 block 5 中我们使用了 x，并且在 block 4 中定义它。由于支配树构建算法总是假设所有的执行路径都是可能实现的，因此完全可能在没有定义 x 的时候就使用了 x。对于 [5] 处的 ADD 指令，我们可以找到它的支配树深度最深的输入来自 [4.1] 中对 x 的赋值，如果单纯执行上面的算法，那就有可能会把 ADD 指令添加到 block 4 里去，这显然是错误的（要知道，我们是先得到支配树后，才依此计算 CFG，上图中左图的 CFG 是一个正确结果的展示，实际上在执行这一步时，我们不知道有这样一个 CFG），它错误的根源在于 block 4 并没有支配 block 5。

我们的解决方案是利用 SSA 转换时留下的一些“额外的” phi 指令。为什么它们会被移除呢？是因为在和 GCM 往往一起进行的优化 GVN 中，我们会进行恒等式优化把这种 phi 指令给优化掉，关于它的详细信息可以在有关 GVN 和 LVN 的文章中查看。对于上面的代码，如果使得这些额外的 phi 指令可见，会长成这样：

1
2
3
4
5
6
7
8
9
10
11

int first := TRUE, x0 := T, sum0 := 0;	[1]
while (pred()) {	[2]
	sum1 := phi(sum0, sum2);	[2.1]
	x1 := phi(x0, x3);	[2.2]
	if (first) {	[3]
		first := FALSE;	[4]
		x2 := ...;	[4.1]
	}
	x3 := phi(x1, x2);	[5]
	sum2 := sum1 + x3;	[5.1]
}

本质上， 的声明会将其初始化为未定义的值 T。然后，这个值会与赋给 x 的其他值合并，合并需要 phi 指令。这些 phi 指令就支配了 block 5 中 x 的使用，如此，ADD 指令就可以被正确地放置到 block 5 中去了。

这个问题也会出现在循环之外。我们考虑一段这样的代码：

1
2
3
4
5
6
7
8
9

int x0 := T, z0 := ...;	[1]
if (sometime()) {	[1.1]
	x1 := ...;	[2]
	x2 = phi(x0, x1);	[3]
}
if (sometime_later()) {	[3.1]
	y := z0 + f(x2);	[4]
	...y...	[5]
}

它会得到如下的支配树和 CFG：

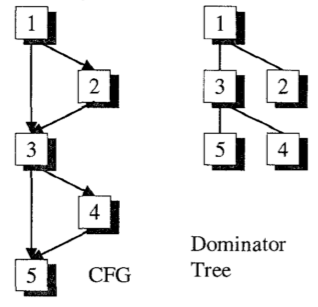
block 3 处的 phi 指令非常关键。如果我们将其作为额外的 phi 移除，那么本应该在 block 4 中的 f(x) 的计算将被提前调度到 block 2 中。

从这两个例子中我们可以总结出：这些额外的 phi 指令不能被移除，因为它们保存着有关值的可用性的关键信息。在我们实现 GVN 算法的过程中，我们会使用类似 x = phi(x, T) 这样的恒等式优化来移除这种 phi 指令，这种移除事实上是不合适的，我们需要对其进行特判。

讨论最后块

上一步讨论会把代码提升得太多，我们不能够将其作为最终的结果——它得到的代码大部分是预测性质的，生命周期太长。一个经典的现象是它会把所有的常量都提升到程序的开头（原因是计算支配树的时候会把它们提升），或者使得指令使用了还没被定义的变量（比如把 load 指令搞到了使用它的 add 后面）不管它们的第一次使用是在什么地方。因此我们还需要讨论指令能够放置的最后的块。这样一来，在最前块和最后块之间将得到一个合适且合法的范围，以供我们放置指令。

这里需要复习一个图论概念：最近公共祖先（Lowest Common Ancestor, LCA）。我们希望找到支配树中所有指令使用的 LCA。对于每条指令，寻找 LCA 可能需要 的时间，但事实上这个数也挺小的。依旧是从固定指令开始，我们对指令的所有 uses 使用后序 DFS，在访问（并将它们调度到最后块去）了一个指令的所有孩子后，我们再来调度指令本身。在调度之前，我们经过上一步讨论，将指令调度到最前的合法块中，此时它的 uses 的 LCA 就代表了它的最后块。此时，很显然最前块是支配着最后块的（当然，前提是没有移除那些额外的 phi 指令，这个一定要注意），在支配树中有一条从最前到最后块的线，它表示着可以放置指令的安全范围，我们可以把指令放在这条线上的任何块中。那么应该选择哪个块呢？我们选择处于最浅循环嵌套中最近（也就是说最依赖于控制）的位置。

对于大多数指令来说，uses 产生在与指令本身相同的块中。然而，对于 phi 指令显然不是这样，往往可以再往上回溯。

下面给出讨论最后块的算法伪代码：

在这个地方，我们需要注意关于 uses 的叙述，虽然比较显然，但笔者一开始也搞糊涂了：第一段中的 uses 指的是 UsedValue，比如 ret %1 中的 %1；而第二段中讨论的 uses 则是指令的 user。因为你想，我们的目的是讨论出指令能放置的最后位置，固定指令的形式注定了它们不会有 user（除了 PHI，不过从伪代码可以看出它被特殊讨论了），因此第一段的循环里讨论的是 usedValue；而对于一个指令，最显然的“最后”位置肯定是使用了它的固定指令前面，但一个指令可能有多个使用者，因此我们讨论所有使用了它的固定指令的公共祖先，作为它的“最后块”计算结果。总结而言就是不要照抄伪代码，要考虑清楚 LLVM 的细节。

其实使用 use 这个叙述多半是有点渊源的。因为在 LLVM 里，Use 是一个关于使用者和被使用者的 Pair，而笔者的项目里并没有为 Use 单独建立数据结构，因此导致了自己一开始的混淆。

笔者的代码大致如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

for (Instruction instruction : instructionList) {
    if (isPinned(instruction)) {
        visited.add(instruction);
        for (Value input : instruction.getUsedValues()) {
            if (input instanceof Instruction) {
                scheduleLate((Instruction) input);
            }
        }
    }
}    

/* ...... */

private void scheduleLate(Instruction instruction) {
        if (visited.contains(instruction) || isPinned(instruction)) {
            return;
        }
        visited.add(instruction);
        BasicBlock lca = null;

        for (User user : instruction.getUsers()) {
            if (user instanceof Instruction) {
                Instruction userInst = (Instruction) user;
                scheduleLate(userInst);
                BasicBlock useBB = userInst.getParent();
                if (userInst instanceof Phi) {
                    // Reverse dependence edge from i to y
                    // Use matching block from CFG
                    /* ...... */
                }
                lca = findLCA(lca, useBB);
            }
        }
	/* ...... */
    }

有关寻找 LCA 的部分就不赘述了。

选择目标块放置指令

在上一节中，我们已经谈过选择目标块的标准。这里讨论一些额外的问题。当我们为指令选择好最终的位置后，我们可能会影响到其他指令的合法位置，尤其是我们通过代码提升操作把指令提出循环的时候。为了解决这种交互式的影响，我们提出以下的算法：

也就是说，在寻找最后块的时候，我们就敲定好指令最终放置的位置。这也是为什么原论文将目标块的选择标准放到了上一节去讨论。

参考：

• Cliff Click, Global Code Motion Global Value Numbering, 1995
• Thomas Lengauer, Robert Endre Tarjan, A Fast Algorithm for Finding Dominators in a Flowgraph, 1979